Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 65
Um membro comprimido de comprimento de flambagem igual a 2,3m é obtido conectando-se com parafusos duas cantoneiras de 127 x 7 x 12,7 conforme mostrado. Usando o método por tensões admissíveis, determine a carga axial centrada para a coluna. Use e .
Passo 1
Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo, mas antes vamos ao nosso esboço :D
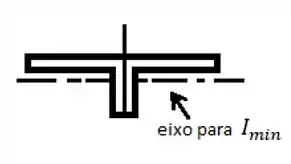
Para um ângulo de aço, o apêndice C fornece
Passo 2
Para a coluna feita usando os dois ângulos como mostrado,
Aço:
Transição:
Passo 3
Carga central permitida:
Resposta
Exercícios de Livros Relacionados
Uma força centrada de 80,1 kN é aplicada a uma coluna retangular de madeira serrada com 6,71m de comprimento de flambagem. Usando madeira serrada para a qual a tensão admissível ajustada à compressão
Um elemento de compressão com 9m de comprimento de flambagem é obtido soldando-se duas placas de aço com 10mm de espessura a um perfil de aço laminado W250 x 80, conforme mostre a figura. Sabendo que
Para uma haste feita com a liga de alumínio 2014-T6, selecione a menor seção transversal quadrada que pode ser usada se a haste suporta uma carga centrada de 55 kip.
Uma força centrada de 72 kN precisa ser suportada por uma coluna de alumínio conforme mostra a figura. Usando a liga de alumínio 6061-T6, determine a dimensão b mínima que pode ser usada.
Uma coluna com 6,4m de comprimento efetivo é obtida conectando quatro cantoneiras de aço L89 x 89 x 9,5mm com barras de travamento conforme mostrado. Utilizando método das tensões admissíveis, determi