Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 70
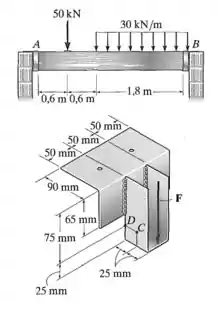
O suporte de parede tem espessura de 6 mm e é usado para suportar as reações verticais da viga carregada, como mostra a figura. Se a carga for transferida uniformemente para cada alça do suporte, determine o estado de tensão nos pontos C e D da alça B. Considere que a reação vertical F nessa extremidade age no centro e na borda do suporte, como mostra a figura.
Passo 1
Precisamos das reações em B.
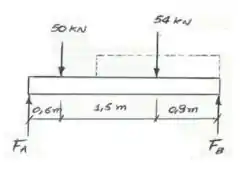
Por somatório de Momento:
Passo 2
Assim precisamos do momento atuando na alça:
Passo 3
Calcular as tensões.
Onde C é a distância horizontal entre o ponto C e o centroide da peça (0) e o mesmo para D.
Vale ressaltar que as tensões cisalhantes são iguais zero nos dois pontos.
Resposta
Exercícios de Livros Relacionados
Uma força vertical de 400l b é aplicada em D em uma engrenagem fixada ao eixo sólido A B de 1i n de diâmetro. Determine as tensões principais e a tensão de cisalhamento máxima no ponto H localizado no
A força P centrada é aplicada a um pilar curto conforme mostrado. Sabendo que as tensões no plano a - a são σ = - 15k s i e τ = 5k s i , determine (a) o ânguloβ que o plano a - a forma com a horizonta
Um mecânico usa um pé de cabra para soltar um parafuso em E . Sabendo que o mecânico aplica uma força vertical de 24l b em A , determine as tensões principais e a máxima tensão de cisalhamento no pont
Um tubo de aço A B tem 102m m de diâmetro externo e espessura da parede de 6m m . Sabendo que o braço C D é rigidamente conectado ao tubo, determine as tensões principais e a tensão máxima de cisalham
Duas forças de 5,34k N são aplicadas a um elemento de máquina AB em forma de L, conforme mostrada a figura. Determine as tensões normal e de cisalhamentos (a) no ponto a ,(b)no ponto b ,(c)no ponto c.