Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 75
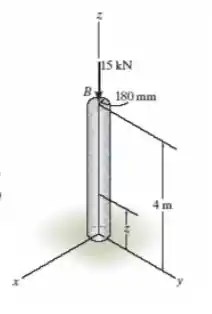
A coluna é feita de concreto de densidade e está sujeita a uma força de compressão axial de em sua extremidade superior . Determine a tensão normal média na coluna em função da distância medida em relação à base. Observação: por causa da deformação localizada nas extremidades, o resultado servirá apenas para determinar a tensão normal média em uma seção removida das extremidades da coluna.
Passo 1
Falaaa! Vem comigo!
Antes de começar, vamos fazer uma observação: o enunciado possui um errinho na unidade da densidade. Para chegarmos no valor dado pelo gabarito, precisamos usar e não , belezinha? Continuando...
Desejamos calcular a tensão normal média em função de . Devemos lembrar, então, que a tensão normal é dada por
Onde
resultante da força normal;
Área da seção transversal da barra;
Para o nosso caso a área da seção transversal é dada por um círculo de raio . Aí essa área fica constante:
Precisamos então achar a expressão de em função de . Não se assusta com isso de calcular em função de , vamos chegar lá juntos. Bora!
Passo 2
Cara, a gente precisa entender qual é a força normal interna resultante nessa coluna. Bora fazer um DCL? A gente vai imaginar que a seção onde a gente quer descobrir é a seção onde a coluna se apoia no chão. Então temos:
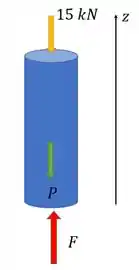
Sendo a força normal nessa seção. Vemos que a força normal resultante é a soma de com o peso da coluna fazendo a equação de equilíbrio para o eixo :
Masss, ele não quer que a gente considere simplesmente o peso de toda a coluna.
Ele quer o peso de uma coluna que esteja distante do chão. Sendo que não pode ultrapassar a altura máxima da coluna. Por que isso?
Cara, ele diz que esse resultado só vale para seções que não sejam extremidades da coluna, por isso não podemos ter e também não podemos analisar essa coluna saindo de Se não estaríamos considerando a extremidade inferior, beleza?
Então, o que temos, é esse pedacinho da coluna:
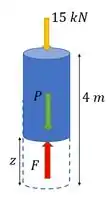
Aí você pode imaginar que está ali nessa nova seção (onde começa a coluna azul na altura ).
E aplicando a equação de equilíbrio na vertical novamente, vemos que a força resultante vai continuar sendo
Mas precisamos achar esse .
Passo 3
Repara que o pedaço de coluna tem altura . Aí podemos achar o peso desse pedacinho de coluna usando essa fórmulinha:
Sendo que é a gravidade, a densidade e o volume da coluna. E volume é dado pelo produto entre área da base e altura . Substituindo nossos dados:
Aí a resultante fica:
Portanto, nossa tensão normal média em função de será