Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 50
O corpo de prova falhou no ensaio de tração a um ângulo de 52° sob uma carga axial de 100 kN. Se o diâmetro do corpo de prova for 12 mm, determine a tensão de cisalhamento média e a tensão normal média que agem na área do plano de falha inclinado. Determine também qual a tensão normal média em atuação sobre a seção transversal quando acorreu a falha.
Passo 1
Bora desenhar a seção onde tudo rola, e aí a gente vai poder enxergar melhor.
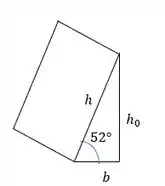
Maneirinho, repara que o nosso ângulo de 52 graus se repete aqui embaixo pois as faces superior e inferior da peça são paralelas.
A força normal precisa ser perpendicular ao plano, então a gente vai decompor ela:
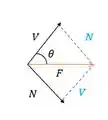
Onde
Detalhe que aqui, você pode desenhar tanto as forças do lado direito da seção quanto do lado esquerdo, nesse caso eu as desenhei do lado direito, com F saindo da seção.
E:
Passo 2
Agora, devemos calcular a área da seção inclinada, que será a área circular decomposta com o ângulo de inclinação:
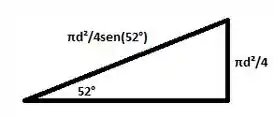
Calculamos então a área:
E a área inclinada:
Passo 3
Com a área e as forças atuantes no plano inclinado, podemos calcular as tensões neste plano:
Começando pela tensão normal:
Substituindo:
E a tensão cisalhante:
Substituindo:
Já a tensão média nas seções tranversais verticais da peça, a gente só precisa calcular qual a tensão média que atuava na peça, sabendo a força normal (dada no enunciado) e a área da seção reta da peça que também já foi calculada.
E aí