Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 52
A junta está submetida a uma força axial de . Determine a tensão normal média que age nas seções e . Considere que o elemento é liso e tem de espessura.
Passo 1
Fala aí galerinha do responde aí, tudo de boa? Bora estudar mais um pouco.
Queremos as tensões normais médias nesssa duas seções dentro da peça, a e . Para determinar a tensão média, precisamos achar as forças internas normais resultantes em cada seção.
Para fazer isso, a gente vai cortar nossa peça nessas duas linhas que definem as duas seções e posicionar as forças normais nelas, assim:
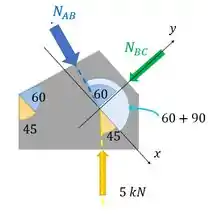
O ângulo de dá a orientação da seção em relação a vertical. Por isso, a força de faz 45 graus com essa seção (que colocamos a orientação coincidindo com ).
Já o ângulo de é a orientação da seção . Ele faz graus com (a seção ), e a força normal na seção faz com , logo ela faz com com . Por isso que a gente tira que o ângulo dela em relação a é .
Passo 2
Depois aque a gente saca melhor essa geometria, precisamos aplicar a equação de equilíbrio para cada eixo e achar o valor das forças normais e .
O somatório das forças no eixo x tem que ser zero, então teremos:
Usamos seno para porque o ângulo dela é oposto ao eixo . E cosseno para porque o ângulo dela está colocado nesse eixo. Isolando a força:
A mesma linha de racicionio faremos em Y.
Substituindo o valor de e fazendo as contas:
Passo 3
Para calcular a tensão média, precisamos determinar as áreas de cada seção. Ela serão o produto entre o comprimento da seção e a expesssura da junta:
Passo 4
Agora, é fazer a força sobre a área para achar a tensão média.
Em AB:
Em BC: