Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 37
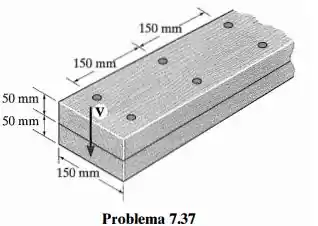
A viga é construída com duas tábuas presas uma à outra na parte superior e na parte inferior por duas fileiras de pregos espaçados de 150 mm. Se uma força de cisalhamento interna for aplicada às tábuas, determine a força de cisalhamento à qual cada prego resistirá.
Passo 1
Vamos usar o primeiro passo para agrupar os dados da questão!
A questão nos fornece os seguintes dados:
- A base da seção transversal é:
- A altura de cada placa de madeira é:
- O espaçamento entreos pregos:
- A força de cisalhamento:
A questão pede o valor da força que atua sobre o prego
Passo 2
Essa é uma viga simétrica, então podemos garantir que o centroide é bem no meio da seção!
Então podemos calcular o momento de inércia sem dificuldades.
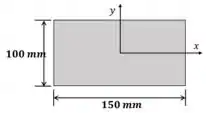
Como a seção é retangular, a equação do momento de inércia é:
Passo 3
Nas questões de cisalhamento com parafuso, esta é a hora que costumam acontecer os erros.
Vamos calcular o momento estático começando no topo da viga até o ponto em que as duas placas se unem.
O desenho abaixo destaca a região em laranja:
E agora calculamos o momento estático multiplicando a área laranja vezes o centroide da região laranja:
Passo 4
E agora a gente tem que saber qual é o fluxo de cisalhamento que atua na região de contato entre as duas placas de madeira.
A fórmula do fluxo de cisalhamento é:
Vamos aplicar os valores:
Logo, ofluxo de cisalhameto é:
Passo 5
Agora vamos calcular a força que atua em cada prego!
Mas antes a gente precisa saber: “Quantos pregos resistem ao fluxo de cisalhamento?”
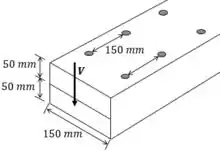
Veja na figura abaixo:
Observe que o à medida que o fluxo de cisalhamento avança ao longo da viga, ele é resistido por DOIS pregos de cada vez!
Assim, podemos definir o fluxo de cisalhamento como:
O número dois aparece na equação acima porque o fluxo de cisalhamento enfrenta dois pregos de cada vez.