Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 51
Um corpo de prova sob tração com área de seção transversal A é submetido a uma força axial P. Determine a tensão de cisalhamento média máxima no corpo de prova e indique a orientação θ de uma seção na qual ela ocorre.
Passo 1
Oláaa, querido!
Então, ele quer saber a tensão de cisalhamento máxima que pode haver nesse elemento e em que seção (qual orientação da seção inclinada) essa tensão máxima ocorre.
Bem, uma forma de a gente resolver essa é escrever a tensão de cisalhamento em uma seção inclinada, de orientação genérica . E depois ver para qual valor de vamos ter o maior valor da tensão.
E aí a gente precisa começar achando a carga de cisalhamento resultante na nossa seção inclinada.
Para fazer isso, precisamos cortar nossa peça na seção inclinada, escolher um lado e fazer o diagrama de corpo livre da situação nova. Vamos cortar nosso elemento em um plano que faz com a horizontal e olhar só para a esquerda. Assim:
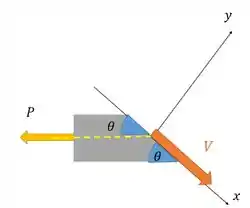
Aí percebe que a gente posiciona nessa seção o vetor que representa essa força interna. A força de cisalhamento deve ser paralela a seção.
O sentido dos vetores aqui é mais arbitrário mesmo, tá? Cê escolhe. O importante é respeitar os referenciais que escolher nas continhas. Vamos seguir!
Passo 2
Agora é utilizar as equações de equilíbrio na direção e achar.
Passo 3
Aí a gente quer achar a tensão média de cisalhamento. A tensão média é dada pela razão entre carga e área da seção onde ela é aplicada. Repara que só falta a gente achar a área da seção então para usar achar a tensão.
O desenho da seção fica dessa forma.
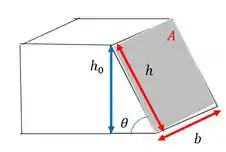
Onde são as dimensões da seção transversal da peça. A força vai atuar no plano inclinado (área sombreada), de área:
Sendo que podemos achar usando trigonometria:
E a área fica:
Passo 4
Agora é calcular a expressão da tensão de cisalhamento:
Substituindo nossas expressões de e
Agora vamos refletir. e são dimensões da peça, logo elas não mudam, são constantes. Então apenas varia com . E percebe que ela é proporcional ao produto entre seno e cosseno.
Podemos pensar aqui na identidade trigonométrica:
Substituindo isso na expressão da tensão:
Agora nossa tensão é proporcional apenas ao seno. O maior valor de seno é , ele ocorre quando o argumento do seno vale . Para que isso aconteça ali, o valor de deve ser
Então é aí é onde ocorre o cisalhamento máximo.
Passo 5
Bem, ele quer o valor dessa tensão máxima. E só temos como dados o e a área transversal da peça .
Vamos olhar nossa expressão da tensão:
Lembra que dissemos que é a largura da seção transversal da peça e é a altura da seção transversal da peça. Percebe que a área transversal da nossa peça pode ser escrita como
Subtituindo isso na expressão da tensão:
E a tensão máxima ocorre em :