Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 46

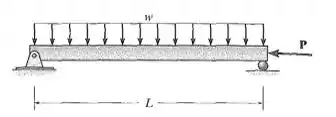
A coluna ideal tem peso w e permanece na posição horizontal quando sujeita a uma carga axial P. Determine o momento máximo no ponto médio do vão da coluna. EI é constante.

Passo 1

A equação do momento será:

M x = w 2 x 2 - L x - P v

Logo:

E I d 2 v d x 2 = w 2 x 2 - L x - P v

Teremos a seguinte EDO:

d 2 v d x 2 + P v E I = w 2 E I x 2 - L x

A solução será do tipo:

v = C 1 s e n P E I x + C 2 c o s P E I x + w 2 P x ² - w L x 2 P - w E I P 2

Sabemos que as condições de contorno são:

x = 0 → v = 0

x = L 2 → d v d x = 0

Teremos:

C 1 = w E I P 2 t g P E I   L 2

C 2 = w E I P ²

Logo, a equação da linha elástica é dada por:

v = w P E I P t g P E I   L 2 s e n P E I   x + E I P cos ⁡ P E I   x + x 2 2 - L x 2 - E I P

Logo, para x = L 2 :

v m á x = w E I P 2 sec ⁡ P E I L 2   – P L 2 8 E I - 1

Portanto:

M m á x = - w E I P sec ⁡ P E I   L 2 - 1

Resposta

v m á x = w E I P 2 sec ⁡ P E I L 2   – P L 2 8 E I - 1

M m á x = - w E I P sec ⁡ P E I   L 2 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a carga máxima P que pode ser aplicada ao elemento estrutural BC sem provocar flambagem no elemento estrutural AB. Considere que AB é feito de aço e que suas extremidades estejam presas por
Uma coluna de madeira serrada com seção transversal de 190,5 x 139,7mm tem um comprimento de flambagem de 5,49m. Sabendo que, para o tipo de madeira utilizado, a tensão admissível ajustada à compressã
Um elemento de compressão tem a seção transversal mostrada na figura e comprimento de flambagem de 1524mm. Sabendo que a liga de alumínio usada é a 2014-T6, determine a carga centrada admissível.
A barra AB está livre em sua extremidade A e engastada na base B. Determine a força P centrada admissível se a liga de alumínio for (a) 6061-T6 ou (b) 2014-T6.
Um perfil de aço laminado W200 x 46,1 é usado para formar uma coluna com comprimento de flambagem de 6,4 m. Usando o método da tensão admissível, determine a força centrada admissível se a tensão de e