Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 158
A viga-caixão é feita de um material elástico perfeitamente plástico para o qual σe = 250 MPa. Determine a tensão residual nas partes superior e inferior da viga após a aplicação e posterior remoção do momento plástico Mp.
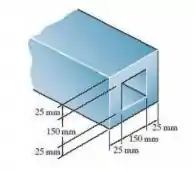
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa viga com material plástico com essa tensão de 250 MPa. Então, precisamos encontrar as tensões residuais na parte de cima e na de baixo nos instantes antes e depois de Mp. Partiu??
Passo 2
Ok, nós vamos começar pensando na barra. Ela é retangular e sem nenhum tipo de anomalia no meio, certo?? Então, nossa linha elástica será bem no meio, e as nossas forças de tração (Tn) e contração (Cn) serão iguais aos pares, ou seja:
(mais na borda) (mais para o centro)
Sabendo disso, vamos calcular nosso T1 (ou C1, como preferir) inicial.
Agora, vamos calcular nosso T2 (ou C2, tira aí no par ou ímpar).
Passo 3
Pronto!! Agora vamos jogar tudo lá na nossa formulinha e teremos o nosso momento.
Com o nosso momento achado, vamos descobrir a nossa tensão máxima e a variação de tensão.