Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 106
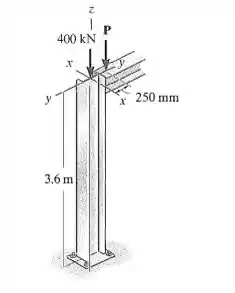
A coluna W310 67 de aço estrutural A-36 suporta uma carga axial de 400 kN além de uma carga excêntrica P = 300 kN. Determine se a coluna falhará com base nas equações AISC da Seção 13.6 e Equação 13.30. Considere que a coluna está engastada na base e que seu topo está livre para oscilar no plano x-z enquanto preso por pinos no plano y-z.
Passo 1
Fala aí galera, borá fazer mais um problema de resmat.
Ele pede para a gente descobrir se essa coluna de aço vai aguentar esse carregamento, usando as equações AISC da Seção 13.6 e a 13.30, que é essa
As propriedades dessa seção e do aço são tabeladas:
Para o eixo , como ela está engastada e livre, . Já para , ela está engastada e presa por pinos, então
tem uma excentricidade em relação ao eixo , .
Agora vamos usar essas equações que ele pediu para resolver esse problema.
Passo 2
Para saber que fórmula usar, vamos calcular o índice de esbeltez limite pela fórmulinha:
Devemos separar os dois eixos e verificar o maior índice de esbeltez:
Em x-z:
Em y-z:
Aí usamos o valor que ficou no intervalo:
Na fórmulnha:
Vemos que quem está nesse intervalo é o de :
Essa é a tensão admissível para a nossa coluna.
Passo 3
Agora, vamos calcular a tensão na coluna e ver se fica maior ou menor que a admissível.
Sabemos que nossa tensão máxima é dada por:
Sabemos que o momento é a força vezes a excentricidade. Ele está em torno de :
O é a distância máxima do nosso eixo neutro que é :
vai ser a soma das duas forças aplicadas:
Substituino nossos dados na fórmula da tensão:
Como a tensão máxima na viga é maior que a admissível, temos que essa coluna vai falhar.
Resposta
A coluna falha.