Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 88
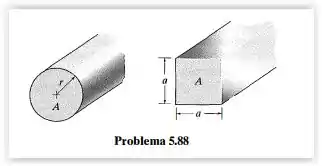
Compare os valores da tensão de cisalhamento elástica máxima e do ângulo de torção desenvolvidos em eixos de aço inoxidável com seções transversais circular e quadrada. Cada eixo tem a mesma área de seção transversal de comprimento de e está submetido a um torque de .
Passo 1
Olá, pessoal! vamos ao trabalho!!
A questão quer que comparemos os valores da tensão de cisalhamento elástica máxima e do ângulo de torção para dois eixos de seções transversais diferentes.
Os dados que foram fornecidos:
Para aço inoxidável , .
Com a área é fácil calcular a dimensão do raio e da aresta .
Vamos logo calcular o momento polar de inércia para agilizar.
Seção circular:
Passo 2
Primeiro vamos calcular a tensão de cisalhamento máxima.
Para a seção quadrada temos que a tensão de cisalhamento máxima é dada pela formula abaixo, retirada da tabela do livro:
Para uma seção circular utilizaremos a fórmula já conhecida.
Passo 3
Agora vamos calcular o ângulo de torção, a começar pela seção quadrada:
A fórmula para o ângulo de torção de uma seção quadrada pode ser encontrada na mesma tabela da tensão de cisalhamento máxima.
Agora para a secção transversal circular;