Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 129

Complete a dedução da Eq. 8.15 que relaciona as trações nas duas partes de uma correia em V .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos o seguinte diagrama da vista lateral de uma pequena seção do cinto:

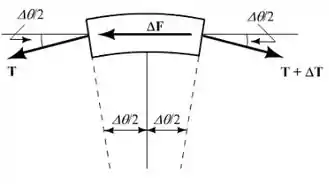
Vamos agora desenhar a vista final de uma pequena seção da correia:

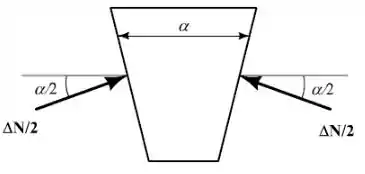
Temos que:

∑ F y = 0

2 ∆ N 2 s e n ⁡ α 2 - T + T + ∆ T sen ⁡ ∆ θ 2 = 0

∆ N = 2 T + ∆ T sen ⁡ α 2 sen ⁡ ∆ θ 2

Passo 2

O somatório das forças em x nos dá:

∑ F x = 0

T + ∆ T - T cos ⁡ ∆ θ 2 - ∆ F = 0

Logo:

∆ F = ∆ T cos ⁡ ∆ θ 2

Quando houver escorregamento iminente, temos que:

∆ F = μ s ∆ N

Logo:

∆ T cos ⁡ ∆ θ 2 = μ s 2 T + ∆ T sen ⁡ α 2 sen ⁡ ∆ θ 2

Dividindo os dois lados por ∆ θ , temos que:

∆ T ∆ θ cos ⁡ ∆ θ 2 = μ s 2 T + ∆ T ∆ θ sen ⁡ α 2 sen ⁡ ∆ θ 2

Passo 3

Podemos então aplicar o limite ∆ θ → 0 e resolver:

Temos que:

d T d θ = μ s T sen ⁡ α 2

d T T = μ s sen ⁡ α 2 d θ

Intefrando, temos que:

∫ T 1 T 2 d T T = ∫ 0 β μ s sen ⁡ α 2 d θ

ln ⁡ T 2 T 1 = μ s sen ⁡ α 2 β

Portanto, a equação que relaciona a tensão nas duas partes da correia V é:

T 2 T 1 = e μ s β sen ⁡ α 2

Resposta

T 2 T 1 = e μ s β sen ⁡ α 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

125- Resolva o Problema 8.124 , considerando que o horário M O é aplicado ao tambor.
124- Uma barra A E de 45N é suspensa por um cabo que passa por um tambor de 125m m de raio. O movimento vertical na extremidade E é impedida por dois batentes mostrados na figura. Sabendo que μ s = 0.
120- Um cabo passa em torno de três tubos paralelos. Sabendo que os coeficientes de atrito são μ s = 0.25 e μ k = 0.20 , determine ( a ) o menor peso W para o qual o equilíbrio é mantido, ( b ) o maio
122. Uma fita de gravação passa sobre o tambor de acionamento B de 20m m de raio e sob o tambor esticador C . Sabendo que os coeficiente de atrito entre a fita e os tambores são μ s = 0,40 e μ k = 0,3
101. Uma amarra é enrolada com duas voltas completas em torno de um poste de amarração. Exercendo uma força de 360N na extremidade livre da amarra, um estivador consegue resistir a uma força de 22,5k