Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 122
122. Uma fita de gravação passa sobre o tambor de acionamento de de raio e sob o tambor esticador . Sabendo que os coeficiente de atrito entre a fita e os tambores são e e que o tambor é livre para girar, determine o menor valor admissível de para que a fita não escorregue sobre o tambor .
Passo 1
Bom! Vamos lá para mais um probleminha sobre correias. Sendo assim, qual é a primeira coisa que temos que fazer?
Ora bolas! Já tá meio que repetitivo, mas é o procedimento padrão; tá? Temos que fazer o diagrama de corpo livre para o nossos sisteminha. Vamos lá!
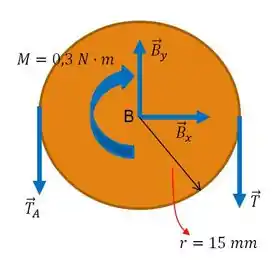
Então, baseado nessa beleza de imagem, façamos o somatório dos momentos em relação ao ponto . A fita gira no sentido horário; por isso, usemos uma convenção negativa de momento:
Passo 2
E agora que já fizemos o diagrama de corpo livre e também obtivemos uma coisinha interessante, bora utilizar a velha relação que conhecemos para o atrito em correias na condição iminente de deslizamento:
Onde é a tração máxima, que nomearemos de e é a tração mínima, que chamaremos de . E como estamos trabalhando com condição de iminência temos que o valor de , é igual a . Já o ângulo , que é o ângulo subentendido pelo arco do tambor sobre a qual a correia está enrolada, ao olhar a figura percebemos que vale ou radianos. Sendo assim, obtemos que:
Que beleza! Sabe por quê? Já obtivemos no que:
E então, obtemos :
Mas e o valor da força ? Ora bolas! Pela figura do enunciado, podemos ver claramente que a força é na verdade o que utilizamos, né não!? Mas que perda de tempo! Sendo assim: