Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 124
124- Uma barra de é suspensa por um cabo que passa por um tambor de de raio. O movimento vertical na extremidade é impedida por dois batentes mostrados na figura. Sabendo que entre o cabo e o tambor, determine o maior binário no sentido anti-horário que pode ser aplicado no tambor se o deslizamento não ocorre, a força correspondente aplicada na extremidade da barra.
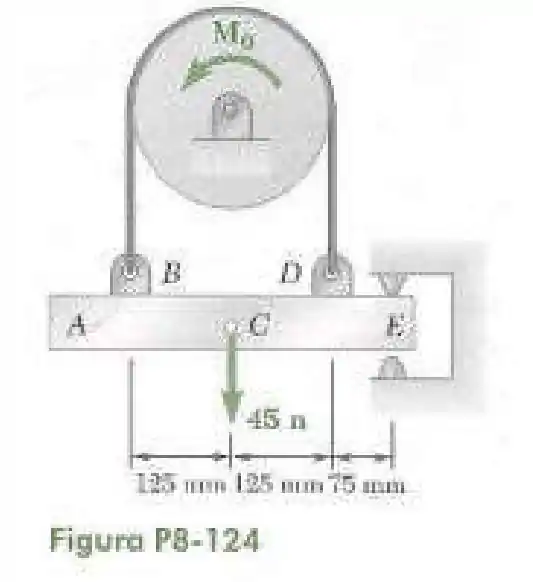
Passo 1
Se fizermos o diagrama de forças que ocorrem somente entre a barra e o tambor nós teremos:
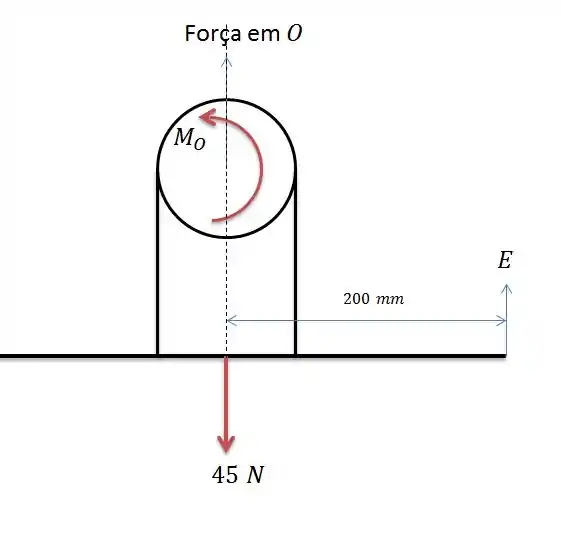
Fazendo a somatória dos momentos onde a força de exerce a força vale:
Agora analisando somente as forças nas barras nós teremos:
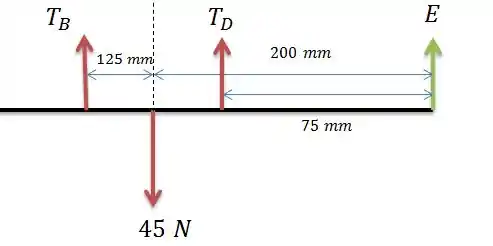
Dessa forma fazendo a equação de momento em nós chegamos na seguinte equação.
Passo 2
Agora analisando as forças na polia.
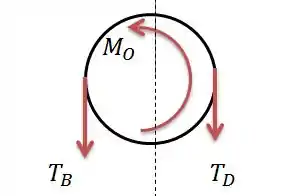
Para esse momento não significar rotação então quer dizer que é maior que , nos dando a seguinte formula de forças com ângulo de abraçamento igual a .
Logo:
Então será:
Passo 3
Então o valor de se encontra pela somatória das forças verticais na barra.
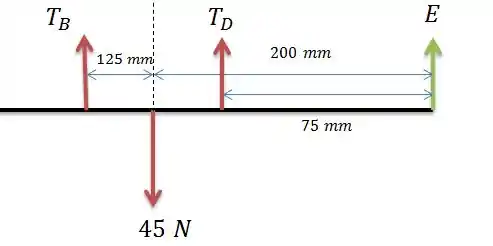
Força que terá sentido para baixo.
E consequentemente o valor de será: