Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 35

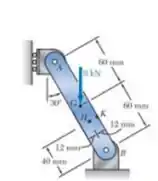
A componente AB tem uma seção transversal retangular uniforme de 10   ×   24   m m . Para o carregamento mostrado, determine as tensões normal e de cisalhamento (a) no ponto H e (b) no ponto K.

Passo 1

E aí gurizada, vamos começar nossos cálculos? Vamos considerar o esboço abaixo :D

⨮ ∑ M B = 0 :       ( 120   c o s   30 ° ) R A - ( 60   s i n   30 ° ) ( 9 ) = 0

R A = 2,598   k N + ↑ ∑ F y = 0                 B y - 9 = 0

B y = 9   k N ↑ → + ∑ F x = 0                         2,598 - B x = 0             B x = 2,598   K n

Passo 2

Na seção que contém os pontos H e K:

P = 9   c o s   30 ° + 2,958   s i n   30 ° = 9,093   k N

V = 9   c o s   30 °   -   2,958   s i n   30 ° = 2,25   k N

M = ( 9 × 10 3 ) ( 40 × 10 - 3   s i n   30 ° ) - ( 2,598 × 10 3 ) ( 40 × 10 - 3   c o s   30 ° ) = 90   N / m

Agora devemos determinar a área para calcular a inercia ;)

A = 10 × 240 = 240   m m 2 = 240 × 10 - 6   m 2

I = 1 12 ( 10 ) ( 24 ) 3 = 11,52 × 10 3   m m 4 = 11,52 × 10 - 9   m 4

Passo 3

No ponto H:

σ x = - P A = - 9,093 × 10 3 240 × 10 - 6

σ = 37,9   M p a

τ x y = 3 2 V A = 3 2 2,25 × 10 3 240 × 10 - 6

τ = 14,06   M p a

No ponto K:

σ x = - P A - M c I = - 9,093 × 10 3 240 × 10 - 6 - 90 12 × 10 - 3 11,52 × 10 - 9

σ = 131,6   M P a

Resposta

(a) σ = 37,9   M p a   e τ = 14,06   M p a

(b) σ = 131,6   M P a e τ = 0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque esférico pressurizado deverá ser fabricado com aço de 12 mm de espessura. Se for submetido a uma pressão interna p=1,4 Mpa, determine seu raio externo para que a tensão normal máxima não ult
Em um tanque esférico de gás tem raio interno r = 1,5m . Se for submetido a uma pressão interna p = 300k P a , determine a espessura exigida para que a tensão normal máxima não ultrapasse 12M P a .
Resolva o problema 8.78 se a seção transversal for quadrada de dimensões 6mm por 6mm
A viga de abas largas está sujeita à carga mostrada na figura. Determine as componentes da tensão nos pontos A e B e mostre os resultados em um elemento de volume em cada um desses pontos. Use a fórmu
O pino de suporte sustenta a carga de 3,5 kN. Determine as componentes da tensão no elemento estrutural do suporte no ponto A. O suporte tem 12 mm de espessura.