Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 148
Mostre que a soma das três medidas de deformação feitas com uma roseta de 60° é independente da orientação da roseta e igual a
Em que é a abscissa do centro do círculo de Mohr correspondente.
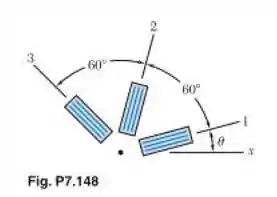
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar a equação 7.44 vista nesse capítulo, que nos dá a deformação ao longo de um eixo qualquer, dada por:
E vamos utilizar essa relação nas 3 direções, lembrando que aqui estamos lidando com deslocamentos no círculo de Mohr, então para cada 60° de rotação na roseta, temos 120° no círculo. Fazendo isso, chegaremos em expressões para as direções 1, 2 e 3, depois disso é só substituir as expressões e simplificar para chegar na relação dada no enunciado. Então bora lá!
Passo 2
Beleza! Antes de começar, vamos só escrever a tensão média, que será dada por:
Ok!! Agora, vamos escrever a deformação na direção 1, que está a um ângulo da referência, utilizando a equação vista no passo 1. Então teremos:
Substituindo a expressão para a deformação média, chegamos em:
Beleza! Vamos guardar essa expressão aqui por enquanto. Agora vamos escrever a deformação na direção 2, que está a uma rotação de da referência, então teremos:
Agora, vamos substituir a expressão para a deformação média e abrir as somas de arco, então teremos:
Essa será nossa segunda equação, vamos guardar ela também.
Passo 3
Agora, vamos escrever a expressão para a deformação na direção 3, que está a uma rotação de da referência, então teremos:
Agora, vamos substituir a expressão para a deformação média e abrir as somas de arco, então teremos:
Essa é a nossa terceira expressão. Tá legal! Agora vamos começar somando a segunda e terceira expressões, para cancelarmos alguns termos, fazendo isso, teremos:
Agora vamos somar a parcela referente a , chegando em:
Observe que os termos com e possuem sinais opostos, então a equação acima se reduz a:
Que é exatamente a equação dada no enunciado! Shoow, conseguimos mais um!
Resposta
Ei, a resposta está no passo a passo :)