Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 85

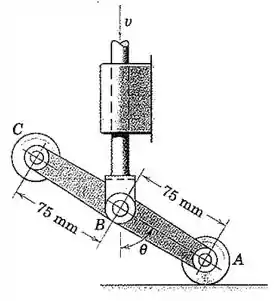
Os componentes de um dispositivo de comutação são mostrados. Se a haste de controle vertical tem uma velocidade descendente v = 0,9 m / s quando θ = 60 ° e se o cilindro A está em contato com a superfície horizontal, determine o módulo da velocidade C para este instante.

Passo 1

Vamos relacionar os dados da questão com a Figura do enunciado. É dito que a haste vertical possui v = 0,9 m / s . Então, sendo uma barra rígida e sem rotação, todos os pontos desta haste possui a mesma velocidade. E vale dar uma atenção especial ao ponto B, pois ele também é um ponto da haste inclinada. Portanto, v = V B . Além disso, como A está apoiado no que vamos chamar de chão, sua velocidade deve estar na horizontal. Portanto, vamos representar os vetores velocidade no desenho esquematizado para facilitar a visualização do problema.

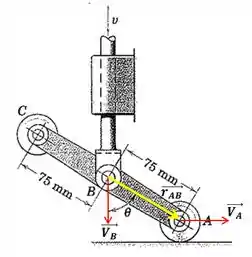
Outro vetor que vai ser importante nesta questão é o vetor posição r A B → . Isso porque o enunciado já dá o valor de seu módulo e o ângulo com a vertical.

Bom, o enunciado quer saber a velocidade de C, então pra que perder tempo com B e com A?

Vamos lá! Sabendo as velocidades de A e B, é possível calcular a velocidade relativa entre os pontos e consequentemente, a velocidade angular ω   da barra AC. Uma vez conhecendo esta ω , conseguimos enfim calcular a velocidade de C, V C . Ainda confuso? Então vem comigo.

Passo 2

Nesta etapa, vamos usar a equação da velocidade relativa.

V A → = V B → + V A / B → = V B → + ω → × r A B →

Onde   r A B → = 0,075 m

Como V A   e   V B são perpendiculares entre si, fica mais simples decompor a equação acima em i ^   e   j ^ , já que sempre vai ter um termo que vale zero. Em relação a j, temos:

V A   j ^ = V B j ^ + ω k ^ × r A B →   i ^

0   j ^ = - 0,9 j ^ + ω k ^ × 0,075 s e n 60 °   i ^

0   j ^ = - 0,9 j ^ + 0,065 ω   j ^

ω → = 13,85   k ^   r a d / s

Decompondo em i ^ :

V A   i ^ = V B i ^ + ω k ^ × r A B →   j ^

V A   = 0 i ^ + 13,85 k ^ × ( - 0,075 c o s 60 ° )   j ^

V A   = 0   i ^ + 0,52   i ^ = 052   i ^   m / s

Passo 3

Nesta etapa o ponto C finalmente vai entrar na história. Vamos fazer a mesma coisa que na etapa anterior, mas usando as equações da velocidade relativa V A / C . Então:

V A → = V C → + V A / C → = V C → + ω → × r A C →  

Onde   r A C → = 0,15 m

Decompondo novamente a expressão em i ^   e   j ^ :

V A   j ^ = V C j ^ + ω k ^ × r A C →   i ^

0   j ^ = V C j ^ + 13,85 k ^ × 0,15 s e n 60 °   i ^

0   j ^ = V C j ^ + 1,8   j ^

V C j ^ = - 1,8   j ^   m / s

Decompondo em i ^ :

V A   i ^ = V C i ^ + ω k ^ × r A C →   j ^

0,52   i ^ = V C i ^ + 13,85 k ^ × ( - 0,15 c o s 60 ° )   j ^

V C i ^ = - 0,52   i ^   m / s

Portanto, o módulo de V C é dado por:

V C = - 1,8 2 + - 0,52 2  

V C = 1,873   m / s

Esta questão possui diversas formas de ser resolvida. A apresentada não é a mais curta, porém abrange o conteúdo de uma forma bem interessante.

Resposta

V C = 1,873   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um mecanismo para empurrar pequenas caixas de uma linha de montagem para uma correia transportadora é mostrado com o braço OD e a manivela CB em suas posições verticais. A manivela gira no sentido hor
No instante representado, a = 150 mm e b = 125 m, e a distancia a + b entre A e C está diminuindo na taxa de 0,2 m/s. Determine a velocidade em comum V dos pontos B e D para esse instante.
O mecanismo é parte de um dispositivo de engate onde a rotação do elemento AOB é controlada pela rotação do elemento ranhurado D em torno de C. Se o membro D possui uma velocidade angular no sentido h
Os elementos do mecanismo para a implantação da lança do magnetômetro de uma nave espacial são mostrados. Determine a velocidade angular da lança quando o elemento de acionamento OB ultrapassa o eixo
A roda rola sem deslizar. Para o instante representado, quando O está diretamente sob o ponto C, a barra AO possui uma velocidade V = 1,5m/s para a direita e θ = 30 ° . Determine a velocidade angular