Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 89
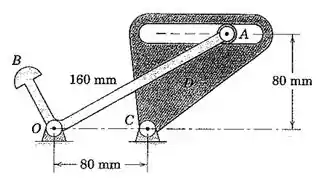
O mecanismo é parte de um dispositivo de engate onde a rotação do elemento AOB é controlada pela rotação do elemento ranhurado D em torno de C. Se o membro D possui uma velocidade angular no sentido horário de 1,5 rad/s quando a ranhura está paralela a OC, determine a velocidade angular correspondente de AOB. Resolva gráfica ou geometricamente.
Passo 1
No mecanismo mostrado na questão, o elemento AOB irá deslizar pela ranhura de D. Portanto, existe um ponto E coincidente a A neste instante que pertence ao ranhurado D.
Nestes exercícios, é importante fazer um esboço mais simples com os dados da questão, pois ajuda a visualizar melhor. Vamos a ele:
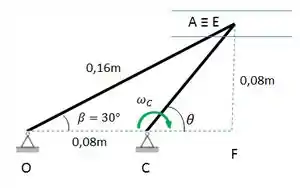
Olha só como ajudou:
Pelo triângulo formado pela linha tracejada em azul, OFE, a gente pode ver que o ângulo , tirado da relação , e ainda que
Por Pitágoras, encontramos que e pelo triangulo retângulo CFE encontramos o que ângulo
Passo 2
Nesta etapa, vamos calcular as velocidades.
Como foi dito anteriormente, existem dois pontos coincidentes A e E, em que A se encontra na haste AO e o ponto E se encontra no ranhurado D. Isto é muito importante para definir as direções das velocidades.
A haste AO é fixa em O, portanto é perpendicular a AO. O ranhurado D é fixo em C, portanto é perpendicular a CE. E ainda digo mais, a velocidade relativa se encontra na ranhura, pois é onde ocorre o deslizamento.
Vamos fazer um desenho esquemático para melhor visualização:
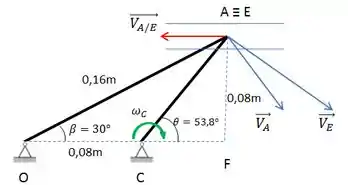
Podemos iniciar os cálculos:
Passo 3
Agora, vamos esboçar os vetores velocidades da equação:
Agora peço que olhe com muita atenção a Figura abaixo. Lembrando mais uma vez que é perpendicular a AO e é perpendicular a CE. Desta maneira fica mais fácil visualizar os ângulos:
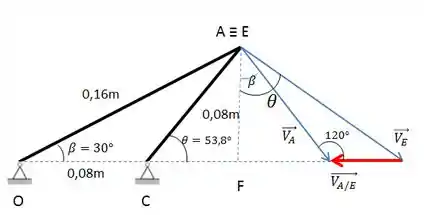
Agora que já foi mostrado de onde saíram os ângulos, vou isolar apenas os vetores, para ter uma Figura mais limpa.
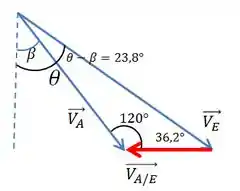
Aplicando a Lei dos Senos:
Do Passo 2, temos a relação:
Então: