Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 87

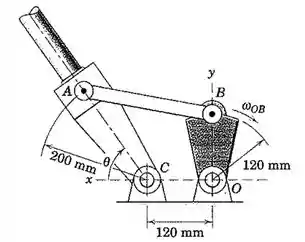
Os elementos do mecanismo para a implantação da lança do magnetômetro de uma nave espacial são mostrados. Determine a velocidade angular da lança quando o elemento de acionamento OB ultrapassa o eixo y com uma velocidade angular ω O B = 0,5 r a d / s se t a n θ = 4 / 3 neste instante.

Passo 1

Então pessoal, primeiro é importante colocar os dados na Figura para conseguir visualizar melhor o que o enunciado pede. A questão quer saber a velocidade angular ω A C , dados a velocidade angular de OB   ω O B   e   t a n θ = 4 3   →   s e n θ = 4 5 ; c o s θ = 3 5 . Também é dado que OB está saindo da vertical neste instante. Melhor dizendo, a barra OB neste instante está passando pelo eixo y, porém ainda está nele.

Então, antes de desenhar os vetores velocidade, vamos observar quais pontos seriam interessantes e onde eles se situariam. Bom, como a haste AB faz a ligação entre a lança AC e a barra OB, é uma boa ideia observar o comportamento dos pontos A e B. Com isso podemos já esboçar suas velocidades. Lembrando: como estes pontos fazem parte de uma barra fixa em um ponto articulado (C ou O), os Vetores velocidade V A   e   V B estarão perpendiculares aos segmentos A C   - e   O B - respectivamente. Vamos ao esboço:

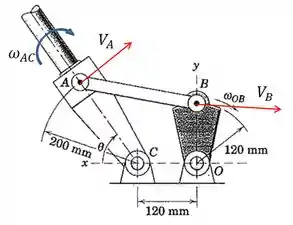
Para descobrir a velocidade angular ω A C , a gente pode ver que fica fácil se encontrar a velocidade do ponto A. Mas para isso, primeiro é preciso estudar todo o mecanismo e seus vetores.

Então vamos lá!

Passo 2

Por ser uma questão de mecanismo, vamos precisar usar muitas relações entre vetores. Então fica mais fácil fazer um esboço do mecanismo com todos eles.

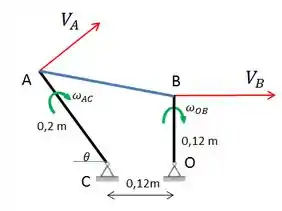
Deste esquema, podemos escrever os seguintes vetores posição:

r A C → = - 0,2 c o s θ   i ^ + 0,2 s e n θ   j ^ = - 0,2 ∙ 3 5 i ^ + 0,2 ∙ 4 5 j ^ = - 0,12   i ^ + 0,16   j ^

r B O → = 0   i ^ + 0,12   j ^

r A B = - 0 , 1 2 + 0,2 c o s θ i ^ + 0,2 s e n θ - 0,12 j ^ = - 0,12 + 0,2 ∙ 3 5 i ^ + 0,2 ∙ 4 5 - 0,12 j ^

r A B → = - 0 , 24   i ^ + 0 , 04   j ^

Passo 3

Agora, vamos entrar com os vetores velocidade. Podemos calcular V B com os dados do enunciado:

V B → = ω O B   k ^ × r B O → = - 0,5 k ^ × 0,12 j ^

V B → = 0,06 i ^   m / s

Podemos escrever a velocidade V A da mesma forma:

V A → = ω A C   k ^ × r A C → = - ω A C k ^ × ( - 0,12 i ^ + 0,16 j ^ )

V A → = 0,16 ω A C   i ^ + 0,12 ω A C   j ^

E ainda, podemos escrever a velocidade relativa V A / B deste modo:

V A / B → = ω A B   k ^ × r A B → = - ω A B k ^ × ( 0,24 i ^ + 0,04 j ^ )

V A / B → = 0,04 ω A B   i ^ - 0,24 ω A B   j ^

Passo 4

Bom, nesta etapa iremos calcular as velocidades angulares. Para isto, precisamos relacionar as velocidades de A e B com a velocidade relativa. Para isso usamos a equação:

V A = V B + V A / B

Substituindo os valores:

0,16 ω A C   i ^ + 0,12 ω A C   j ^ = 0,06 i ^ +   0,04 ω A B   i ^ - 0,24 ω A B   j ^

Para melhorar a visualização e os cálculos, vamos decompor a equação acima nas direções i ^   e   j ^ :

0,16 ω A C   i ^ = 0,06 i ^ +   0,04 ω A B   i ^

0,12 ω A C   j ^ = 0,24 ω A B   j ^

Resolvendo o sistema, encontramos o resultado final:

ω A B = 0,214   r a d / s

ω A C = 0,429 r a d s ; s e n t i d o   H

Resposta

ω A C = 0,429 r a d s ; s e n t i d o   H o r a r i o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16.93. Se a extremidade A do cilindro hidráulico está se deslocando com uma velocidade V A = 3 m / s , determine a velocidade angular da barra B C no instante mostrado.
No instante mostrado, o caminhão se desloca para a direita de 3m / s , enquanto o tubo rola no sentido anti-horário a ω = 6r a d / s sem deslizar em B. Determine a velocidade do centro G do tubo.
16.91. Se é dada uma velocidade V o = 10m / s ao centro O da engrenagem, determine a velocidade do bloco deslizante B no instante mostrado.
16.96. Se C tem uma velocidade V C = 3 m / s , determine a velocidade angular da roda no instante mostrado.
16.89. Se o segmento C D tem uma velocidade angular ω C D = 6 r a d s , Determine a velocidade do ponto E no segmento B C e a velocidade angular do segmento A B no instante mostrado.