Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 92

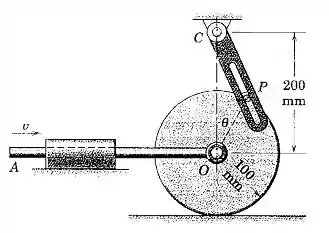
A roda rola sem deslizar. Para o instante representado, quando O está diretamente sob o ponto C, a barra AO possui uma velocidade V = 1,5m/s para a direita e θ = 30 ° . Determine a velocidade angular ω da haste ranhurada.

Passo 1

Nesta questão, temos o movimento do centro da roda e precisamos saber a velocidade angular da haste ranhurada ω .

Primeiramente, vamos estabelecer um ponto D coincidente a P, mas que pertença a haste. Isto é muito comum em questões que apresentam esse tipo de mecanismo com ranhura, pois é possível fazer uma análise mais detalhada e obter relações interessantes.

Como de costume, vamos fazer um diagrama deste mecanismo apresentando alguns de seus vetores.

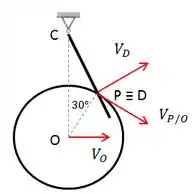
Para obter mais dados para o desenvolvimento da questão, vamos analisar o triângulo COP:

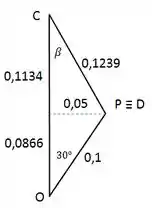
Por Pitágoras, calculamos os segmentos de CO e CP. Podemos ainda encontrar o ângulo β :

tan ⁡ β = 0,05 0,1134 →   β = 23,8 °

Passo 2

Nesta etapa, vamos calcular as velocidades.

V D → = V P → + V D / P →

V P → = V O → + V P / O →

V P / O = ω P O × P O - = V O P O - × P O - = V O

As velocidades podem ser separadas nas direções i ^   e   j ^ . Com a ajuda das Figuras anteriores, podemos representar os vetores da seguinte maneira:

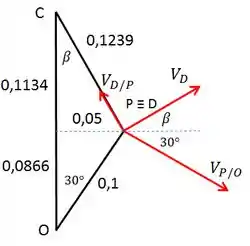
Decompondo as velocidades:

V D → = V D c o s β   i ^ + s e n β   j ^ = 0,915 V D i ^ + 0,403 V D   j ^

V P / O → = V P / O c o s 30 °   i ^ - s e n 30 °   j ^ = 0,866 V P / O i ^ - 0,5 V P / O j ^

A velocidade V D / P está na direção da ranhura:

V D / P → = V D / P - s e n β   i ^ + c o s β   j ^ = - 0,403 V D / P   i ^ + 0,915 V D / P j ^

Passo 3

No último passo, vamos relacionar as equações encontradas acima.

Juntando V P → = V O → + V P / O → e V P / O = V O = 1,5 com a equação   V P / O → encontrada acima, temos:

V P → = 2,799   i ^ - 0,75 j ^   m / s

Juntando V D → = V P → + V D / P → com os resultados mostrados acima, encontramos:

0 , 915 V D i ^ + 0,403 V D   j ^ = 2,799   i ^ - 0,75 j ^ - 0,403 V D / P   i ^ + 0,915 V D / P j ^

Decompondo, caímos num sistema:

0 , 915 V D i ^ = 2,799   i ^ - 0,403 V D / P   i ^

0,403 V D   j ^ = - 0,75 j ^ + 0,915 V D / P j ^

Resolvendo:

V D = 2,26 m s

V D / P = 1,82 m s

E depois de muito algebrismo, podemos enfim determinar a velocidade angular da haste:

ω = V D C D → = 2,26 0,1239 = 18,22 r a d s   n o   s e n t i d o A H

Resposta

ω = 18,22 r a d s   ; n o   s e n t i d o   A H

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16.88. A roda gira sobre seu cubo sem deslizar na superfície horizontal. Se a velocidade do centro da roda é V c = 0,6 m s , para a direita, determine as velocidades dos pontos A e B no instante mostr
16.95. A roda está rigidamente fixada à engrenagem A , que está engrenada às cremalheiras D e E . Se D tem uma velocidade V D = 1,8m / s e V E = 3 m / s . Demonstre que é necessário que a roda deslize
72. O trem de engrenagens epicicloidal consiste da engrenagem sol A que está engrenada à engrenagem planetária B. Esta tem um cubo interior com a engrenagem C que está fixo em B e engrenado na engrena
73. Se a barra de ligação AB tem uma velocidade angular ω A B = 4r a d / s no instante mostrado, determine a velocidade do bloco deslizante E nesse instante. Também identifique o tipo de movimento de
16.106. A placa quadrada está restringida dentro das ranhuras em A E B . Quando θ = 30 ° , o ponto A está se deslocando com V A = 8 m s . Determine a velocidade do ponto C nesse instante.