Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 91

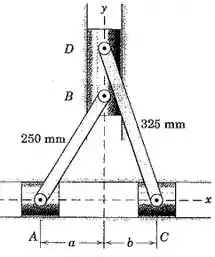
No instante representado, a = 150 mm e b = 125 m, e a distancia a + b entre A e C está diminuindo na taxa de 0,2 m/s. Determine a velocidade em comum V dos pontos B e D para esse instante.

Passo 1

Como já é de costume, primeiro vamos fazer um esboço do mecanismo.

Por Pitágoras, podemos calcular as distâncias OB e OD:

O B = ( 0,25 2 - 0,15 2 = 0,2 m

O D = ( 0 , 32 5 2 - 0,1 2 5 2 = 0 , 3 m

s e n α = 3 5 ; c o s α = 4 5

s e n β = 0,125 0,325 = 5 13 ; c o s β = 0,3 0,325 = 12 13

Os pontos A e C estão se aproximando a uma taxa de 0,2 m/s. Escrevendo de forma vetorial, temos que:

V A - V C = 0,2   m / s

Também é dado que:

V B = V D

Basicamente, estes são os dados mais imediatos que se pode tirar do enunciado.

Passo 2

Agora, iremos entrar na parte de velocidade relativa para relacionar os vetores.

V A = V B + V A / B

V C = V D + V C / D

Subtraindo as equações acima, temos que:

V A - V C = V B - V D + V A / B - V C / D

0,2 = V A / B - V C / D

Agora, vamos fazer um diagrama apenas com os vetores. Lembrando: os vetores velocidade relativa são perpendiculares às barras. Portanto, podemos representar da seguinte forma:

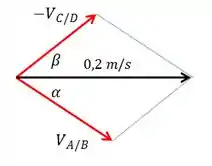
Podemos escrever matematicamente este diagrama:

V A / B   c o s   α + V C / D c o s   β = 0,2  

V A / B   s e n   α - V C / D s e n   β = 0

Resolvendo este sistema, temos que:

V C / D = 0,1 39   m / s

V A / B = 0 , 089   m / s

Substituindo na equação de velocidade relativa:

V A = V B + V A / B ;     o n d e   V = V B

e m   j ^ :     0 = V + V A B   s e n α

V = 0,0535   m / s

Resposta

V = 0,0535   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

62. O pistão P se desloca para cima com uma velocidade de 7,5 m/s no instante mostrado. Determine a velocidade angular do eixo de manivela AB nesse instante.
69. A unidade de bombeamento consiste da manivela AB, barra de ligação BC, balancim CDE e tirante F. Se a manivela está girando com uma velocidade angular ω=10 rad/s, determine a velocidade angular do
61. A rotação da barra de ligação AB cria um movimento de oscilação de engrenagem F. Se AB tem uma velocidade angular ω = 6 r a d s , determine a velocidade angular da engrenagem F no instante mostrad
70. Se o cilindro hidráulico encurta-se a uma taxa constante v C = 0,6m / s , determine a velocidade angular da barra de ligação ACB e a velocidade do bloco B no instante mostrado.
64. O sistema de engrenagem planetária é usado em uma transmissão automática para um automóvel. Ao travar ou soltar determinadas engrenagens, ele tem a vantagem de operar o carro em diferentes velocid