Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 75
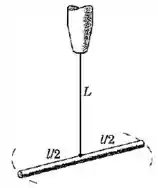
A haste uniforme de comprimento e massa está suspensa em seu ponto médio por um arame de comprimento . A resistência do arame à torção é proporcional ao seu ângulo de rotação e é igual a onde é o momento polar de inércia da seção transversal do arame e é o módulo de elasticidade transversal. Desenvolva a expressão para o período de osiclação da haste, quando é colocada em roação em torno do eixo do arame.
Passo 1
Queremos montar uma equação diferencial que dependa do ângulo de rotação. A melhor forma de fazer isso é através de uma equação de momentos em torno do centro de massa da haste:
O único momento que age sobre o sistema já foi dado no enunciado:
Pode não ser óbvio que corresponde ao momento que o arame exerce sobre o corpo, então vamos dar uma olhada nas unidades de medida para garantir.
No SI, (o momento polar de inércia) é medido em , a elasticidade é medida em (ou ), e o comprimento é dado em , então:
Que a uma unidade do momento no SI. (Lembrando que o radiano é uma unidade adimensional, então não precisams consderar o na nossa análise).
Passo 2
Beleza, agora voltando à nossa equação:
O momento de inércia da haste em relação ao seu centro de massa pode ser consultado em uma tabela:
Vamos escrever isso na forma usual da equação do oscilador harmônico:
E então sabemos que o termo que multiplica é o quadrado da frequência angular :
Como relacionar isso com o período?
Então:
Resposta
O período é .