Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 2
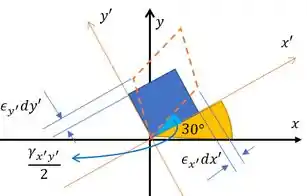
As componentes do estado plano de deformação no ponto da aba da bequilha são , e . Use as equações de transformação da deformação para determinar as deformações equivalentes no plano sobre um elemento orientado a um ângulo de em sentido anti-horário em relação à posição original. Trace um esboço do elemento deformado devido a essas deformações dentro do plano .
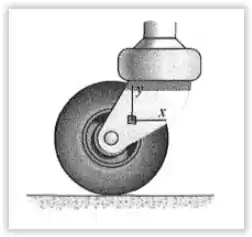
Passo 1
Oláaaa, querido! Cê tá bem?
Então, ele dá o valor das deformações do nosso elemento no plano :
E aí ele quer saber o valor de deformações equivalentes a essa se a gente rotacionar o elemento no sentido anti-horário em relação ao eixo atual.
Ele mesmo fala para gente usar a equação de transformação de deformações. Ou seja, temos fórmulinhas para a gente achar , e , que são as deformações equivalentes do elemento rotacionado.
Vamos usar essas bonitas e partir para o abraço!
Passo 2
A equação de transformação da deformação normal para o eixo tem essa carinha:
Onde é a deformação normal do elemento rotacionado. Vamos dizer que ela está na direção de um eixo que faz com o eixo .
E esse está no sentido horário. Então para o nosso caso .
Então substituindo os valores que a gente nessa fórmulinha, encontramos a deformação em
Passo 3
Agora, repetindo a ideia do passo anterior, alterando apenas a fórmula de transformação de deformação para encontrar :
Esse é a deformação na direção de um eixo , que faz com o eixo .
Vamos substituir nossos valores nessa fórmulinha também:
Passo 4
Utilizaremos agora a equação de transformação da deformação por cisalhamento de um elemento orientado a um ângulo de :
Substituindo nossos dados:
Passo 5
Aí ele pede para a gente esboçar esse elemento com a nossa orientação e suas deformações
Ele vai ter, mais ou menos, a seguinte cara:
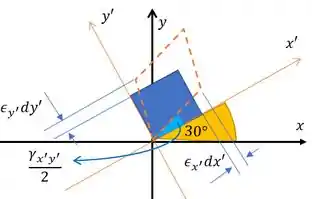
Esse retângulo azul é o elemento sem deformar e o tracejado laranja é ele deformado.
Como a gente monta isso?
Bem, como todas as deformações são positivas, a gente tem que nosso ângulo que representa (entre e aresta do elemento deformado) fica dentro do elemento original.
E as deformações normais são positivas, então o elemento “cresce” nas direções e . Aí a gente marca esse aumento nas bordas mais próximas dos eixo e . Aí fica tudo prontinho!
Resposta
