Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 3
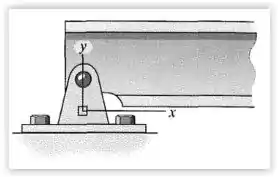
3. As componentes do estado plano de deformação no ponto sobre a aba do pino são , e . Use as equações de transformação da deformação e determine as deformações equivalentes no plano sobre um elemento orientado a um ângulo em sentido anti-horário em relação à posição original. Trace um esboço do elemento distorcido devido a essas deformações no plano .
Passo 1
Utilizando a equação de transformação da deformação normal para o eixo , dado o valor do ângulo .
Substituindo os valores numéricos adequados:
Passo 2
E agora, repetindo a ideia do passo anterior, alterando apenas a fórmula de transformação de deformação pela correspondente à do eixo :
Trocando as variáveis pelos seus valores númericos:
Passo 3
Utilizaremos agora a equação de transformação da deformação por cisalhamento de um elemento orientado a um ângulo de :
Trocando as variáveis pelos seus respectivos números:
Passo 4
Dado que já obtemos as nossas novas deformações nos eixos e , já podemos fazer um esboço do nosso elemento distorcido. Ele vai ter, mais ou menos a seguinte cara:
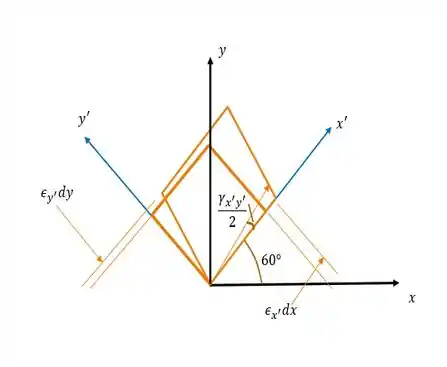
Resposta
A deformação equivalente de um elemento no eixo em um plano rotacionado vale:
A deformação equivalente de um elemento no eixo em um plano rotacionado vale:
A deformação por cisalhamento equivalente de um elemento a um ângulo em um elemento rotacionado é igual a:
