Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 8
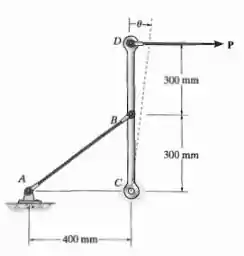
Parte de uma ligação de controle para um avião consiste em um elemento rígido CBD e um cabo flexível AB. Se uma força for aplicada à extremidade D do elemento e provocar uma rotação θ = 0,3°, determine a deformação normal no cabo. Em sua posição original, o cabo não está esticado.
Passo 1
Oláaaa, querido! Tá bem? Então, um cabo AB está inicialmente com comprimento de
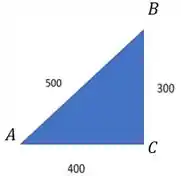
A gente vê isso porque ABC é um triângulo do tipo 3/4/5. Cê também pode usar Pitagoras para achar isso.
Aí ele quer saber qual é a deformação normal nesse cabo se uma força é aplicada em , e essa força causa uma rotação de na haste CD.
Cara, a deformação normal tem essa fórmulinha:
Onde é o comprimento inicia do cabo e é o comprimento final. A gente já tem , então vamos encontrar . Bora!
Passo 2
Antes da deformação, tínhamos algo assim:
Após a deformação, teremos:
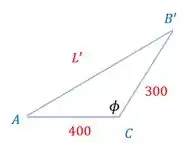
Onde , pois é o ângulo de 90° do triângulo retângulo inicial mais a rotação de causada pelo deslocamento de Além disso, como o ângulo é muito pequeno, podemos considerar o lado como inalterado, ou seja, como os iniciais
Sabendo todos os lados do triângulo (menos o que a gente quer né) e um ângulo dentro do triângulo, podemos usar a lei dos cossenos para achar . Ela vai ter essa carinha:
Isolando :
Passo 3
Agora podemos calcular a deformação usando a nossa fórmulinha:
-3
Resposta
-3