Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 23
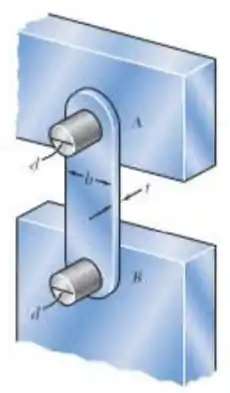
A conexão AB, de largura b = 2 in. e espessura t = 1/4 in., é utilizada para apoiar a extremidade de uma viga horizontal. Sabendo que a tensão normal média na conexão é de -20 ksi e que a tensão de cisalhamento média em cada um dos dois pinos é 12 ksi, determine (a) o diâmetro d dos pinos, (b) a tensão média do rolamento na conexão
Passo 1
E aí gurizada tudo belezinha??? Para encontrarmos o diametro a da capa, partiremos da seguinte equação:
Onde primeiramente devemos encontrar a força:
Agora precisamos encontrar o diâmetro partindo da equação de cisalhamento:
Isolando “d” temos:
Passo 2
b) Agoraaa vamos encontrar a tensão média do rolamento na conexão
Resposta
a)
b)
Exercícios de Livros Relacionados
A viga é apoiada por um pino em A e um elo curto B C . Determine o valor máximo P das cargas que a viga suportará se a tensão de cisalhamento média em cada pino não puder ultrapassar 80M P a . Todos o
O guindaste giratório está preso por um pino em A e suporta um montacargas de corrente que pode deslocar-se ao longo da flange inferior da viga, 0,3m ≤x ≤3,6m . Se a capacidade de carga nominal máxima
A estrutura está sujeita a carga de 1k N . Determine a tensão de cisalhamento média no parafuso em A em função do ângulo da barra θ . Represente essa função em gráfico para 0 ≤ θ ≤ 90 ° e indique os v
A viga é apoiada por um pino em A e um elo curto B C . Se P=15k N , determine a tensão de cisalhamento média desenvolvida nos pinos em A ,BeC . Todos os pinos estão sujeitos a cisalhamento duplo, como
A estrutura de dois elementos está sujeita à carga distribuída mostrada. Determine a maior intensidade w da carga uniforme que pode ser aplicada à estrutura sem que a tensão normal média ou a tensão d