Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 70

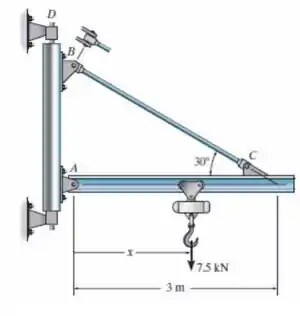
O guindaste giratório está preso por um pino em A e suporta um montacargas de corrente que pode deslocar-se ao longo da flange inferior da viga, 0,3   m ≤   x ≤   3,6   m . Se a capacidade de carga nominal máxima do guindaste for 7,5   k N , determine a tensão normal média máxima na barra B C de 18   m m de diâmetro e a tensão de cisalhamento média máxima no pino de 16   m m de diâmetro em B.

Passo 1

Vamos lá meus camaradas, o que a gente precisa saber para resolver esse problema? precisamos saber quais são as forças que atuam nesse nosso sistema para que então consigamos descobrir quais os valores de tensões normal e de cisalhamento que são dadas por

σ m e d = P A   e   τ m e d = F A c

Com

P: resultante da força normal;

A: Área da seção transversal;

F: Força cortante total;

A c : Área cortante;

Mas para evitar qualquer confusão vamos anotar aqui as constantes dadas no enunciado de acordo com a notação que vamos utilizar na resolução, sendo assim, teremos

P = 7,5   k N ,     x m á x = 3,6 m ,     a = 3 m ,  

θ = 30 ° ,     d b a r = 18 m m ,     d p i n = 16 m m

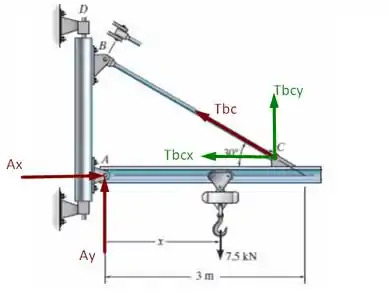
Agora, pra ficar mais claro ainda o que estaremos calculando vamos fazer um diagrama de forças para o nosso problema, dessa forma nós temos

Passo 2

Beleza, agora que temos um plano de ação vamos efetuá-lo para resolver esse exercício, certo? Certo. Primeiramente vamos calcular as reações no suporte A começando pela equação de equilíbrio para o momento (adotando o sentido anti-horário como positivo) dada por

∑ M A = 0

Calculando para as forças que não passam pelo ponto que escolhemos (ponto A ) e que, assim, geram momento vamos ter

T b c ⋅   s e n θ × 3 m - 7,5 k N × ( x )   =   0

T b c ⋅   s e n θ × 3 m = 7,5 k N   ⋅ ( x )  

T b c = 7,5 k N ⋅ x 3 m × s e n ( θ )

Agora, olha essa ideia aqui pra gente pensar um pouquinho: a gente vai ter o valor máximo de F b c quando x for máximo okay? Okay, mas qual o valor de x m á x ? Tá lá nas nossas constantes x m á x = 3,6 m . Portanto,

T b c =   7,5 k N ⋅ 3,6 m 3 m ⋅ s e n ( θ ) = 27 k N 3 ⋅ s e n ( θ ) = 9 k N s e n   θ

Como θ = 30 °

T B C = 9 k N 0,5 = 18 k N

Passo 3

Agora, conseguimos calcular as duas tensões que a questão nos pede, basta calcularmos a área da barra e do pino que são dadas por:

A p i n o = π 4 ⋅ d p i n 2   e   A b a r = π 4 ⋅ d b a r 2

Sendo

d p i n = 16 m m = 16 ⋅ 10 - 3 m

d b a r = 18 m m = 18 ⋅ 10 - 3 m

Assim, vamos ter

A p i n o = π 4 ⋅ d p i n 2 = π 4 ⋅ 16 ⋅ 10 - 3 2 m 2 ≈ 2,01 ⋅ 10 - 4   m 2

A b a r = π 4 ⋅ d b a r 2 = A b a r = π 4 ⋅ 18 ⋅ 10 - 3 ≈ 2,54 ⋅ 10 - 4   m 2

Pronto, temos tudo que é preciso para calcularmos as tensões exigidas pelo problema, mas se liga aí meus camaradas em um detalhe importante: No nosso pino, no desenho do enunciado, podemos ver que ele é fixado por dois pontos, portanto, ocorre ali um cisalhamento duplo! E isso quer dizer para a gente que a força no cálculo da tensão de cisalhamento precisa ser dividida por 2.

τ p i n o = F 2 × A p i n o = T b c 2 × A p i n o = 18 × 10 3 N 2 × 2,01 ⋅ 10 - 4   m 2 ≈ 44.762 M P a

Para a tensão normal não teremos a força divida por dois, então, basta aplicar na sua fórmula normal onde obteremos

σ b a r r a = T b c A b a r r a = 18 k N 2,54 ⋅ 10 - 4   m 2 ≈ 70,736 M P a

Resposta

τ p i n o = 44.762 M P a

σ b a r r a = 70,736 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga é apoiada por um pino em A e um elo curto B C . Se P=15k N , determine a tensão de cisalhamento média desenvolvida nos pinos em A ,BeC . Todos os pinos estão sujeitos a cisalhamento duplo, como
A estrutura de dois elementos está sujeita à carga distribuída mostrada. Determine a maior intensidade w da carga uniforme que pode ser aplicada à estrutura sem que a tensão normal média ou a tensão d
O parafuso longo passa pela chapa de 30 m m de espessura.Se a força na haste do parafuso for 8 k N , determine a tensão normal média na haste, a tensao de cisalhamento média ao longo da área cilíndric
O punção circular B exerce uma força de 2k N na parte superior da chapa A . Determine a tensão de cisalhamento média na chapa provocada por essa carga.
O acoplamento de gancho e haste está sujeito a uma força de tração de 5k N . Determine a tensão normal média em cada haste e a tensão de cisalhamento média no pino A entre os elementos.