A estrutura de dois elementos está sujeita à carga distribuída mostrada. Determine a maior intensidade da carga uniforme que pode ser aplicada à estrutura sem que a tensão normal média ou a tensão de cisalhamento média na seção ultrapasse e, respectivamente. O elemento tem seção transversal quadrada de de lado.
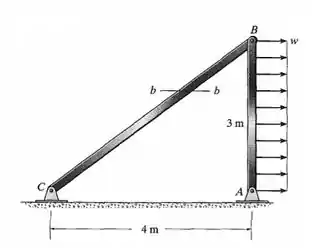
Passo 1
Fala aí meus camaradas, tudo bem por aí? Preparados pra mais uma questãozinha marota?
Vamos lá, primeiramente vamos definir o que desejamos nessa questão: queremos estimar um valor máximo para de tal forma que as tensões de cisalhamento e normal não ultrapassem os valores estipulados pelo enunciado.
Bora deixar anotado aqui os dados fornecidos no enunciado de acordo com a notação que vamos adotar, então, temos
Além disso, como a geometria do problema traz um triângulo é natural pensarmos no teorema de pitágoras para achar algumas medidas úteis para nossa peça. Então fazemos:
Belezinha! A ideia aqui é a gente achar uma expressão paras tensões na seção em função de , e comparar com as tensões admissíveis, tá bem? Aí a gente acha . Bora ver como fazer isso!
Passo 2
Nós temos ali uma carga distribuída, certo? Primeira coisa a fazer é substituir ela por uma carga concentrada equivalente. Aí essa carga é igual a área da carga distribuída, ou seja
E ela está no meio da barra .
Agora a gente precisa resolver essa estrutura aí, encontrando os esforços que passam pela seção .
Olha o que está acontecendo num DCL.
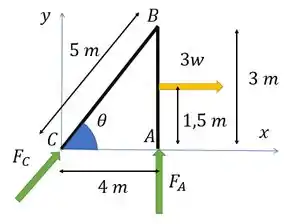
Percebe que a gente só precisa achar o esforço que atua em . E pelo desenho, a gente vê que ele vai ser igual a , a força de reação no ponto , por causa do equilíbrio de forças interno dessa barrinha .
Além disso, para finalizar a etapa de pré-cálculo do problema, vamos decompor a força em , para facilitar nossas continhas, em um componente vertical e um horizontal dados por
Sendo o ângulo em .
Passo 3
Aí a gente quer uma expressão para , né? Pensa comigo. Se a gente usar o somatório de momentos em , a gente a acha direitinho, sem se preocupar com . Bora fazer isso!
Adotando o sentido anti-horário como positivo vamos ter
Daí, como encontramos a componente vertical da força de reação, podemos encontrar o módulo:
E com ela encontrar a componente horizontal:
Essa força será negativa, pois aponta para a esquerda. Com isso, temos nossas forças de reação como:
Passo 4
Esses já são os valores numéricos dos nossos esforços na barra, por causa do equilíbrio interno, lembra? Então, fazendo um esqueminha para ver melhor, nossa barra está assim:
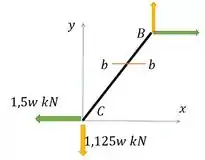
Quem vai gerar esforço normal a nossa seção vai ser a força amarelinha, então:
E quem vai gerar o esforço paralelo a essa seção é a força verde,
Uhul, achamos os esforços!
(Obs.: Como a seção está na horizontal, não precisamos decompor as forças na direção da barra, para encontrar os esforços na seção dada, nos importamos com a direção da seção e não com a direção da barra, por isso que a força normal a seção é a força e a força paralela à seção será a força .)
Passo 5
Achamos a área da nossa seção usando trigonometria também, porque ela está inclinada em relação a seção transversal da barra. Vamos fazer um desenho para entender o que está acontecendo:
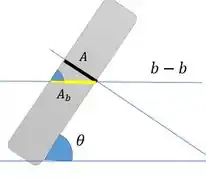
A gente tem que nessa figura, é a hipotenusa de e o cateto oposto dela, então:
E o seno do ângulo, pode ser encontrado fazendo cateto oposto sobre hipotenusa:
Dessa forma vamos obter as seguintes tensões normal e de cisalhamento
Passo 6
A parte mais difícil a gente já encarou, agora tá bem suave se liga aí. Agora é comparar essas tensões que a gente achou com as tensões admissíveis e achar . Assim:
Aí a gente escolhe a menor, já que a carga de causaria uma tensão cisalhante maior do que a admissível. Então nossa resposta final é o segundo .