Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 25
A barra de conexão BD é feita de latão e tem área de seção transversal de . A barra de conexão CE é feita de alumínio e tem área de seção transversal de . Sabendo que elas suportam o elemento rígido ABC, determine a força máxima P que pode ser aplicada verticalmente no ponto A se a deflexão de A não excede 0,35 mm.
Passo 1
Fala aí gurizada tudo belezinha???? Primeiramente antes de calcularmos vamos começar esboçando o diagrama do corpo livre AC.
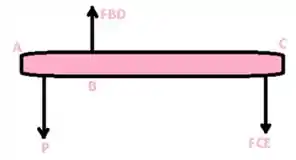
Primeiramente vamos calcular o somatório do momento em C, vem comigo :D
Agora o somatório do momento em B ...
Agora sim gurizada partiu calcular o alongamento na seção B e C:
Passo 2
Fala aí gurizada tudo belezinha? Partiu esboçar o diagrama de deformação.
A partir da Inclinação temos:
Limite de deslocamento
Resposta
Exercícios de Livros Relacionados
As deformações específicas normais determinadas com o uso da roseta da figura, colada na superfície de um componente estrutural, são: ε 1 = - 93,1μ ε 2 = - 385μ ε 3 = + 210μ Determinar: (a) as três de
As deformações específicas normais determinadas com o uso da roseta da figura, colada na superfície de um componente estrutural, são: ε 2 = - 90 × 10 - 6m m / m m ε 3 = - 190 × 10 - 6m m / m m ε 4 = -
O estado plano de tensões mostrado é conhecido na superfície de um componente de máquina, feito de aço de alta resistência. Sabendo-se que E = 200G P a e G = 80 G P a , determinar a orientação e a int
Para a barra do Prob. 6.146, determinar a leitura que poderia ser obtida para vários carregamentos, se o extensômetro estivesse localizado em um ponto diretamente acima, distante 25m m do ponto C , e
Uma barra de aço A B , com 40 × 150m m / m m de seção transversal, suporta uma carga P na extremidade B. Um único extensômetro, formando um ângulo de 45° com a horizontal, é colado à superfície da bar