Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 78

Conforme mostrado na figura, de t = 0 a t = 4 s , a aceleração de uma dada partícula é representada por uma parábola. Sabendo que x = 0 e v = 8 m / s quando t = 0 , (a) construa as curvas v   - -   t e x   - -   t para 0 < t < 4 s , (b) determine a posição da partícula em t = 3 s . (Dica: use a mesa dentro da capa.)

Passo 1

O enunciado pede que a gente determine (a) construa as curvas v--t e x -- t para 0

Dados: Em t = 0 , x = 0 , v = 8 m / s

(a) temos:         v 2 = v 1 +   á r e a   s o b   c u r v a   a - t   d e     t 1   a   t 2

E x 2 = x 1 +   a r e a   s o b   c u r v a   v - t   d e   t 1   a   t 2

Então, usando a fórmula da área da parábola, temos:

e m     t = 2 s :         v = 8 - 1 3 ( 2 ) ( 12 ) = 0

t = 4 s :           v = 0 - 1 3 ( 2 ) ( 12 ) = - 8 m / s

Como a velocidade inicial é igual a 8   m / s , a velocidade é igual a zero em t = 2 s e igual a - 8   m / s em t = 4 .

O que pode ajudar também é reparar que a aceleração tem grau dois (tem t 2 e tals...), então a velocidade, que é a integral da aceleração, vai ter grau três. E isso significa que vai ter a seguinte cara:

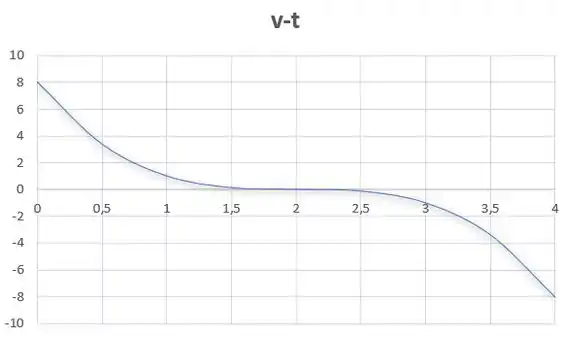
Agora: e m   t = 2 s :               x = 0 + ( 2 ) ( 8 ) 3 + 1 = 4 m

t = 4 s :                             x = 4 - ( 2 ) ( 8 ) 3 + 1 = 0

E continuando o raciocínio pro gráfico da posição, vamos ter grau quatro. E grau quatro é beeeem parecido com o grau 2, quando estamos analisando o formato do gráfico. A diferença é que ele vai ser um pouco mais achatadinho. Então vai ter a seguinte cara:

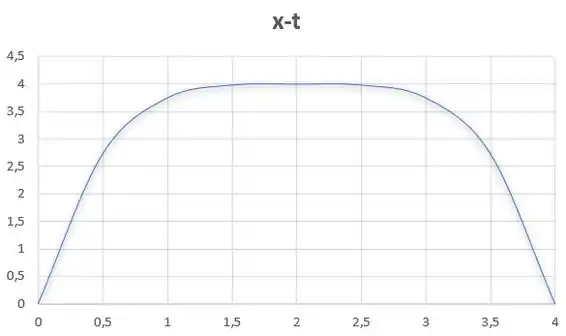
Passo 2

(b) temos:

e m   t = 3 s : a = - 3 ( 3 - 2 ) 2 = - 3 m / s 2

v = 0 - 1 3 ( 1 ) ( 3 ) = - 1 m / s

x = 4 - ( 1 ) ( 1 ) 3 + 1

Ou x 3 = 3.75 m

Resposta

(b) x 3 = 3.75 m

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento de uma partícula sobre a superfície de um cilindro circular reto é definido pelas relações R = A, 2 π t e z = At2/4, onde A é uma constante. Determine as intensidades da velocidade e da ac
O movimento tridimensional de uma partícula é definido por suas coordenadas cilíndricas (veja a Fig. 11.26) R = A/(t + 1), θ = Bt e z = Ct/(t + 1). Determine as intensidades da velocidade e da acelera
Como o motorista de um automóvel viaja para o norte a 25 km/h em um estacionamento, ele observa um caminhão aproximando pelo noroeste. Depois ele reduz sua velocidade escalar para 15 km/h e assim que
O bloco C parte do repouso em t = 0 e move-se para cima com aceleração constante de 25 mm/s2. Sabendo que o bloco A move-se para baixo com velocidade constante de 75 mm/s, determine (a) o instante no
Um irrigador de água oscilante é colocado no ponto A de uma inclinação que forma um ângulo α com a horizontal. O irrigador libera água com uma velocidade v0 em um ângulo ϕ com a vertical que varia se