Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 178

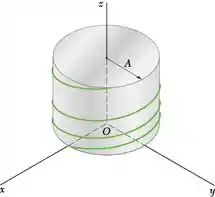
O movimento de uma partícula sobre a superfície de um cilindro circular reto é definido pelas relações R = A, 2 π t e z = At2/4, onde A é uma constante. Determine as intensidades da velocidade e da aceleração da partícula em qualquer instante t.

Passo 1

E ai galera tudo belezinha? O enunciado pede que a gente encontre as intensidades da velocidade e da aceleração da partícula em qualquer instante t.

Nós temos

R = A             θ = 2 π t             z = 1 4 A t 2

Então

R ˙ = 0             θ ˙ = 2 π             z ˙ = 1 2 A t

e

R ¨ = 0             θ ¨ = 0             z ¨ = 1 2 A

Passo 2

v 2 = v R 2 + v θ 2 + v z 2 = R ˙ 0 2 + R θ ˙ 2 + z ˙ 2 = 0 + A + 2 π 2 + 1 2 A t 2 = A 2 4 π 2 + 1 4 t 2

e

a 2 = a R 2 + a θ 2 + a z 2 = R ¨ 0 - R θ ˙ 2 2 + R θ ¨ 0 + 2 R ˙ 0 θ 2 + z ¨ 2 = - A 2 π 2 2 + 0 + 1 2 A 2 = A 2 16 π 4 + 1 4

Resposta

v = 1 2 A 16 π 2 + t 2

a = 1 2 A 64 π 4 + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento de uma partícula é definido pela relação x = 6 t ³ - 8 + 40c o s π t ³ , onde x e t são expressos em milímetros e segundos, respectivamente. Determine a posição, a velocidade e a aceleraçã
O movimento de uma partícula é definido pela relação x = 6 t 4 - 2 t ³ - 12 t ³ + 3 t + 3 ³ ³ , onde x e t são expressos em metros e segundos, respectivamente. Determine o tempo, a posição e a velocid
O movimento de uma partícula é definido pela relação x = 1,5 t 4 - 30 t 2 + 5 t + 10 , onde x e t são expressos em metro e segundos, respectivamente. Determine a posição, a velocidade e a aceleração d
O movimento de uma partícula é definido pela relação x = 2 t ³ - 15 t ² + 2 A t + 4 ³ ² , onde x e t são expressos em metros e segundos, respectivamente. Determine (a) quando a velocidade é zero, (b)
O movimento de uma partícula é definido pela relação x = t ³ - 6 t ² - 36 t - 40 ³ ² , onde x e t são expressos em metros e segundos, respectivamente. Determine (a) quando a velocidade é zero, (b) a v