Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas de Revisão - Ex. 188
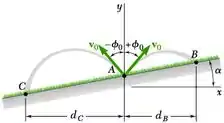
Um irrigador de água oscilante é colocado no ponto A de uma inclinação que forma um ângulo com a horizontal. O irrigador libera água com uma velocidade v0 em um ângulo com a vertical que varia se até . Sabendo que v0 = 9 m/s, = 40° e = 10°, determine a distância horizontal entre o irrigador e os pontos B e C que definem a área molhada.
Passo 1
E ai galera tudo bem? O enunciado pede que a gente encontre distância horizontal entre o irrigador e os pontos B e C que definem a área molhada.
Primeira nota
Além disso, ao longo da inclinação da cabine
Passo 2
Movimento horizontal. (Uniforme)
Movimento vertical. (Movimento uniformemente acelerado)
Substituindo por t
Passo 3
Em B:
ou
Em C:
Resposta
Exercícios de Livros Relacionados
A aceleração de uma partícula é definida pela relação a = - k v onde k é uma constante. Sabendo que x = 0ev = 81m / s em t = 0 ,eq u ev = 36m / s quando x = 18m , determine (a) a velocidade da partícu
Um policial em um carro de patrulha, estacionado em uma zona de 70k m / h de limite de velocidade, observa um automóvel que passa a uma velocidade lenta e constante. Acreditando que o motorista desse
Um caminhão percorre 220me m10s enquanto está sendo desacelerado a uma taxa constante de 0,6m / s ² ². Determine (a) sua velocidade inicial (b) sua velocidade final, (c) a distância percorrida durante
Partindo de x = 0 sem velocidade inicial, uma partícula sofre uma aceleração a = 0,8 v 2 + 49 , onde aev são expressos em m / s ² ² e m / s , respectivamente. Determine (a) a posição da partícula quan
Uma bola de boliche é solta de um barco até que atinja a superfície de um lago com a velocidade de 8m / s . Considerando que a bola experimenta uma desaceleração de a = 10 - 0,9v ² ² quando na água, d