Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 9
O conjunto é composto por duas seções de tubo de aço galvanizado interligadas por uma redução em . O tubo menor tem diâmetro externo de e diâmetro interno de , enquanto o tubo maior tem diâmetro externo de e diâmetro interno de . Se o tubo estiver firmemente preso à parede em , determine a tensão de cisalhamento máxima desenvolvida em cada seção do tubo quando o conjugado mostrado na figura for aplicado ao cabo da chave.
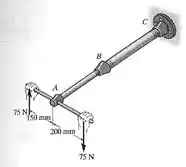
Passo 1
Falaaaa, querido! Tá bem?
Então temos que um conjugado é aplicado em um conjunto feito de tubos de aço. Como esse conjugado gera um momento no eixo dos tubos do conjunto, vamos ter que esse tubos estão sofrendo um torque. E esse torque vai causar tensão de cisalhamento em cada um deles.
Queremos descobrir qual é a tensão de cisalhamento máxima em cada tubo! A fórmulinha da tensão de cisalhamento quando se tem torção é
Onde é o torque atuando na seção, é a distância entre o centro dessa seção e o ponto onde a gente quer a tensão de cisalhamento (na seção) e é o momento polar de inércia. Como nós temos tubos vazados, esse último carinha é dado por
Percebe que quanto maior maior , então a tensão máxima acontece no ponto da seção mais longe do centro, ou seja, na borda dos tubos! Logo, vai ser o raio externo dos nossos tubos.
A ideia é a gente usar essa fórmulinha e achar a tensão máxima em cada trecho desse conjunto. Bora lá!
Passo 2
Vamos começar achando o momento polar de inércia para cada tubo.
Para o tubo menor temos:
- Raio externo: .
- Raio interno: .
- Raio externo: .
- Raio interno: .
Logo, o Momento polar de inércia fica:
Para o tubo maior :
Aí o Momento polar de inércia é:
Passo 3
Os momentos polares de inércia nós já temos . Opa, então o que nos falta saber é o torque em cada tubo!
Vamos procurar esses torques, que age no tubo menor e que age no maior.
Precisamos descobrir qual é o torque acontecendo em cada parte do eixo. O que a gente vai fazer é cortar nosso conjunto em cada um desses trechos e achar o torque atuante na seção.
Para o trecho :
Pelo equilíbrio:
Percebe que o torque gerado pelas forças é oposto ao torque no nosso diagrama, então vamos ter
Passo 4
Agora vamos para o trecho . Vamos fazer uma seção nesse trecho e achar :
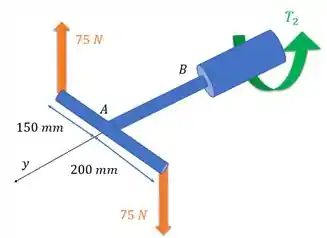
Pelo equilíbrio:
Percebe que o torque gerado pelas forças é oposto ao torque no nosso diagrama novamente, então vamos ter
Passo 5
Agora é usar a fórmula! Primeiro para o tubo menor:
Agora para o tubo maior:
Resposta
Tensão de cisalhamento máxima no tubo menor: .
Tensão de cisalhamento máxima no tubo maior: .