Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 5
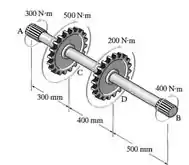
Um eixo maciço de de diâmetro é usado para transmitir os torques aplicados às engrenagens. Determine a tensão de cisalhamento máxima absoluta no eixo.
Passo 1
Mano, o que está acontecendo aí? Vários torques são aplicados em um eixo. E queremos descobrir qual é a tensão de cisalhamento máxima absoluta!
Sabemos que a fórmula da torção para cisalhamento é
Características do eixo:
- Raio do eixo: .
- Momento polar de inércia: .
O é constante pro eixo todo. A tensão máxima vai ocorrer em (distância máxima do centro). Hmmm, então nos falta saber onde ocorre o torque máximo: .
E atente-se que é a tensão máxima absoluta! Ou seja, em módulo! O sinal não importa. Bora lá!
Passo 2
Precisamos descobrir qual é o torque acontecendo em cada parte do eixo.
Primeiro, escolha um sentido do torque pra ser positivo. Vamos escolher o sentido de a para isso. Aponte seu dedão direito nesse sentido. Se o torque seguir seus dedos quando fecham, é positivo. Se não seguir, negativo
Aí quebre o eixo em seções. Vamos por partes, calculando o torque.
- Torque na seção até : .
- Torque na seção até : .
- Torque na seção até : .
Ótimo! Nossa conta fechou com o do final da figura (equilíbrio), então está tudo certo.
O que a gente fez aqui é análogo a desenhar o diagrama de esforços internos para a torção, e ver onde ocorre o torque máximo. Pode fazer assim também, se quiser. Ficaria assim. 😉
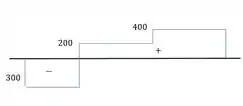
O maior torque ali é (em módulo).
Passo 3
Vamos pra fórmula, achar a tensão que esse gera!
Resposta
Tensão de cisalhamento máxima: .