Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 10
O elo funciona como parte do controle do elevador de um pequeno avião. Se o tubo de alumínio conectado tiver de diâmetro interno e parede de de espessura, determine a tensão de cisalhamento máxima no tubo quando a força de for aplicada aos cabos. Além disso, trace um rascunho da distribuição da tensão de cisalhamento na seção transversal.
Passo 1
Um tubo de alumínio sofre um torque transmitido por um elo
Queremos descobrir qual é a tensão de cisalhamento máxima no tubo!
Sabemos que a fórmula da torção para cisalhamento é
Características do tubo menor:
- Raio interno: .
- Espessura: .
- Raio externo: .
- Momento polar de inércia: .
O conjunto de forças aplicado se equilibra horizontalmente mas causa torção. Essa torção é o carregamento do problema.
Temos o valor de . E pela fórmula dá pra ver que a tensão máxima sempre vai ocorrer na borda do tubo . Opa, então o que nos falta saber é o torque!
Aí depois de achar a tensão máxima, a gente desenha a distribuição da tensão ao longo do raio!
Passo 2
Vamos ver como fica o carregamento
Esse é o único torque no problema! Agora é só aplicar a fórmula!
Passo 3
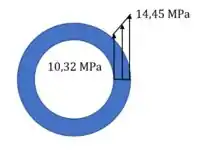
Vejamos a distribuição como fica. Agora vamos desenhar. A fórmula a tensão varia de acordo com o raio! E linearmente!
O máximo da tensão vai ser .
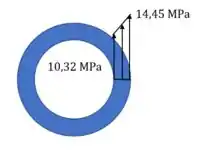
Para calcular aquele valor menor ali na figura, é só usar a fórmula no raio interno.
Resposta
Tensão de cisalhamento máxima: .
