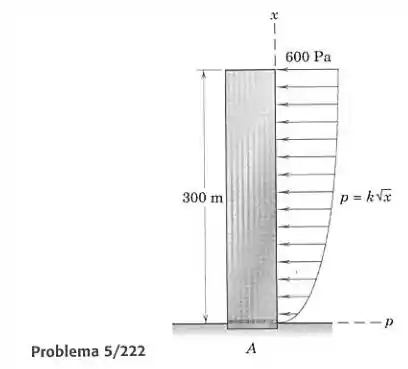
Considere o prédio alto do Prob. 5/222 como uma viga uniforme vertical. Determine a força cortante e o momento na estrutura, e faça um gráfico de ambos, em função da altura acima do chão. Avalie suas expressões para m.
Passo 1
Vamos calcular a força cortante e o momento fletor atuando em uma seção do prédio de altura , isolando em diagrama de corpo livre a parte do prédio que vai da altura até o topo. Isolamos a parte de baixo para evitar a força e o momento causado pela fundação do prédio. Colocamos para a direita e no sentido horário, pela convenção do sentido para o cortante e o momento fletor.
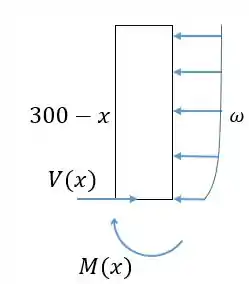
Passo 2
Sabemos pelo Prob. 5/222 que a pressão causada pelo vento na altura é:
Estamos chamando a altura variável de , pois agora é um valor fixo, onde fizemos o corte no prédio, enquanto varia, de até 300 m. Então a força causada pelo vento em um elemento de altura e largura de 60 m é:
Devemos então integrar essa expressão de a 300 m e acharemos a força total causada pelo vento nesse trecho do prédio:
Então, pelo equilíbrio das forças verticais temos :
Passo 3
Para obter , devemos saber o momento em torno da seção de coordenada que a força causada pelo vento causa. A força feita em um elemento de altura em relação à base já foi calculada:
A distância desse elemento até a seção que cortamos , então o momento é dado por:
É importante perceber que aqui é uma constante, e é quem varia! Então, integramos de m a m para saber o momento total causado pelo vento em torno da nossa seção de altura :
Então pelo equilíbrio do corpo o momento fletor terá o mesmo módulo:
Passo 4
Agora vamos representar e em gráficos:


Para , temos: