Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 54
Determine por inspeção, o quadrante no qual está localizado o centro de massa da área sombreada. Determine, em seguida, as coordenadas do centroide. O centro da placa está localizado em M.
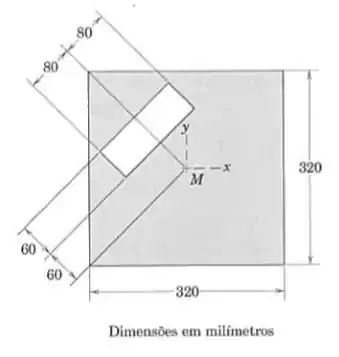
Passo 1
Sabendo que as equações para encontrar o centroide é dado por:
Dessa maneira, vamos primeiro encontrar a área do problema, em forma de tabela!
Passo 2
Primeiro vamos escolher um elemento de área, para assim podermos integrar, mas se analisarmos melhor, nosso problema fica muito mais fácil de dividirmos em várias áreas e calcularmos a soma de cada uma!
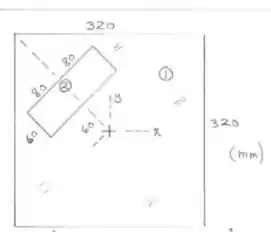
Assim ficando cada área definida acima!!
Passo 3
Vamos então, definir o que é cada área de cada problema!
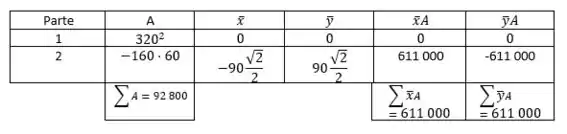
Passo 4
Agora fica bem simples gente, porque podemos voltar para nossa formula original de centroide a partir de área sem integral: