Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas fundamentais - Ex. 1
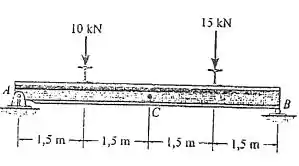
Determine a força normal, o esforço cortante e o momento no ponto .
Passo 1
Para determinar o que se pede, precisamos fazer o diagrama de corpo livre da viga para que seja possível determinar alguma reação externa ao apoio da viga. Após isso, vamos seccionar o corpo no ponto de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas do sistema.
Passo 2
Então, primeiramente, fazendo o diagrama de corpo livre de todo o sistema:
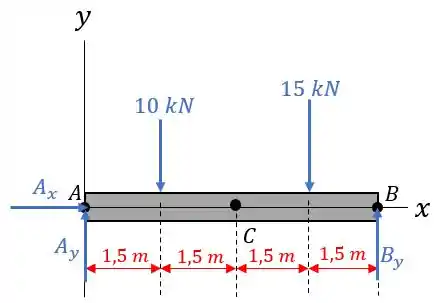
É possível obter a reação exercida no ponto de apoio usando o ponto como referência, tal que, como este ponto possui duas variáveis, elas devem ser “eliminadas” do cálculo para que não haja mais variáveis do que o número de equações.
Logo, aplicando o princípio dos momentos para o ponto e considerando que o momento seja positivo no sentido anti-horário, temos que:
Ou seja:
Portanto:
Passo 3
Em seguida, podemos fazer um “corte” no ponto e dividir a viga em duas partes tal que ambas podem ser analisadas. Pelo fato de o lado direito da viga ter a reação em determinada, ele que será verificado.
Logo, fazendo o DCL dessa seção e mostrando as forças e reações aplicadas, teremos:
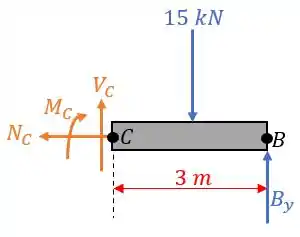
Agora, fazendo o equilíbrio de forças em obtém-se:
Fazendo o equilíbrio de forças em :
Tal que:
Então:
E aplicando o princípio dos momentos no ponto , considerando que o momento é positivo no sentido anti-horário, é possível ter:
Que nos dá:
Ou seja: