Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 17
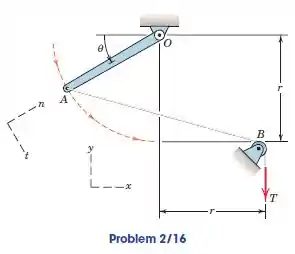
Consulte o mecanismo do problema anterior. Determine uma expressão geral para os componentes e da força trativa aplicada no ponto . Em seguida, avalie sua expressão para e .
Passo 1
Olá, tudo bem com você?
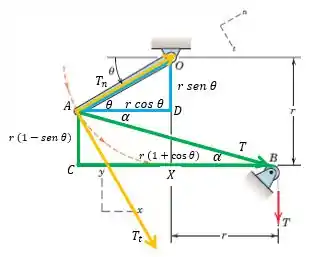
Neste problema, precisamos encontrar as componentes e da força trativa que é aplicada no ponto , sabendo que e . Observe a figura:
Vamos lá!
De início, já vemos que:
Fizemos ali dois triângulos retângulos, vamos falar de cada um deles. Primeiro o triângulo azul:
Veja que a barra tem comprimento igual ao do raio, ,
Então,
Passo 2
Agora, analisando o triângulo verde.
Então,
Veja que,
Portanto,
Olhando para o segmento :
Como :
Passo 3
Queremos o ângulo . Temos e temos , então,
Do enunciado, sabemos que . Substituindo:
Passo 4
Agora só calcular nossas componentes normal e tangencial: