Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 34

Determine a resultante das três forças do Problema 2.21.

Passo 1

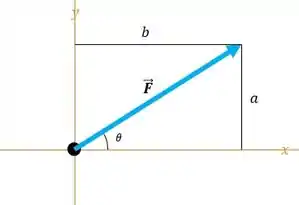
Bom galera, a gente vai encontrar as componentes horizontais e verticais de cada uma das forças que é dada por:

F x = F ⋅ cos ⁡ θ = F ⋅ b b 2 + a 2

F y = F ⋅ sin ⁡ θ = F ⋅ a b 2 + a 2

Passo 2

Show de bola, a gente vai calcular a resultante calculando separadamente a resultante no eixo x e no eixo y :

R x = F 1 x + F 2 x + F 3 x

R x = 800 ⋅ 8 00 600 2 + 800 2 + 408 ⋅ 480 480 2 + 900 2 + 424 ⋅ - 560 560 2 + 900 2

R x = 640 + 192 - 224

R x = 608   N

E agora o eixo y :

R y = F 1 y + F 2 y + F 3 y

R y = 800 ⋅ 6 00 600 2 + 800 2 + 408 ⋅ - 900 480 2 + 900 2 + 424 ⋅ - 900 560 2 + 900 2

R y = 480 - 360 - 360

R y = - 24 0   N

Passo 3

Por último, nós usamos pitágoras para calcular a resultante das forças:

R 2 = R x 2 + R y 2

R 2 = 608 2 + - 240 2

R = 653,65   N

Resposta

R = 653,65   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os cabos de sustentação A B e A C estão presos no topo da torre de transmissão. A força trativa no cabo A B vale 8k N . Determine a força trativa T necessária no cabo A C , tal que o efeito resultante
A placa retangular é composta de quadrados de 1f t , como mostrado. Uma força de 30l b é aplicada no ponto A na direção mostrada. Calcule o momento M O da força em relação ao ponto B por pelo menos do
A tensão no cabo A B é 100N . Determine o momento em relação à O desta tensão aplicada ao ponto A da barra em forma de T . A dimensão b é 600m m .
Consulte o mecanismo do problema anterior. Determine uma expressão geral para os componentes n e t da força trativa T aplicada no ponto A . Em seguida, avalie sua expressão para T = 100N e θ = 35 ° .
Determine os componentes F a e F b com a força de 4k N ao longo dos eixos oblíquos a e b . Determine as projeções de P a e P b de F sobre os eixos a e b .