Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 31
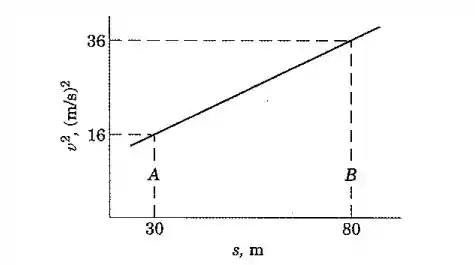
Um corpo que se move em uma linha reta entre dois pontos e afastados de uma distância de tem uma velocidade cujo quadrado aumenta linearmente com a distância percorrida, como mostra o gráfico. Determine o deslocamento do corpo durante os últimos segundos antes da chegada em .
Passo 1
Vamos começar descobrindo qual é a aceleração do corpo:
O problema agora é escrever essa fórmula em função de :
Substituindo isso na equação:
Beleza, agora sabemos que a aceleração é a metade da derivada do gráfico do enunciado.
Passo 2
Vamos calcular essa derivada:
E então a aceleração é:
Queremos calcular o deslocamento nos últimos dois segundos antes do corpo chegar até a posição , para isso precisamos descobir em qual instante (considerado no ponto ) isso acontece:
Como queremos os últimos dois segundos, nosso problema é obter o deslocamento entre e .
Passo 3
Beleza, então vamos ver qual era a velocidade no ponto :
E agora podemos usar a equação de Torricelli para calcular qual distância é percorrida para ir dessa velocidade até a velocidade que ocorre no ponto .
Resposta
O deslocamento do corpo nos últimos dois segundos é de .