Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 35
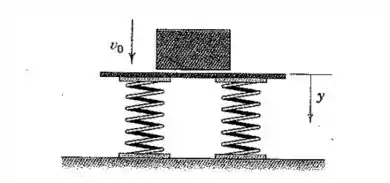
O corpo caindo com velocidade colide e mantém contato com a plataforma apoiada por um jogo de molas. A aceleração do corpo após o impacto é , onde é uma constante positiva e é medido a partir da posição original da plataforma. Se a compressão máxima das molas é observada como , determine a constante .
Passo 1
Depois que o bloco cai sobre as molas, ele vai comprimi-las até , aonde ele para e depois torna a subir, certo?
Isso quer dizer que é o ponto onde a velocidade do sistema é nula. Ou seja, temos duas informações:
Como podemos relacionar essas grandezas?
Passo 2
Vamos integrar os dois lados dessa equação diferencial:
Perceba que o deslocamento vai de até enquanto a velocidade vai de um valor inicial até o zero.
Pronto!
Resposta
A constante vale .
Exercícios de Livros Relacionados
O movimento de uma partícula é definido pela relação x = 6 t 4 - 2 t ³ - 12 t ³ + 3 t + 3 ³ ³ , onde x e t são expressos em metros e segundos, respectivamente. Determine o tempo, a posição e a velocid
O movimento de uma partícula é definido pela relação x = 1,5 t 4 - 30 t 2 + 5 t + 10 , onde x e t são expressos em metro e segundos, respectivamente. Determine a posição, a velocidade e a aceleração d
O movimento de uma partícula é definido pela relação x = 2 t ³ - 15 t ² + 2 A t + 4 ³ ² , onde x e t são expressos em metros e segundos, respectivamente. Determine (a) quando a velocidade é zero, (b)
O movimento de uma partícula é definido pela relação x = t ³ - 6 t ² - 36 t - 40 ³ ² , onde x e t são expressos em metros e segundos, respectivamente. Determine (a) quando a velocidade é zero, (b) a v
O movimento de uma partícula é definido pela relação x = t ³ - 9 t ² + 2 A t - 8 ³ ² , onde x e t são expressos em milímetros e segundos, respectivamente. Determine (a) quando a velocidade é zero, (b)