Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 106
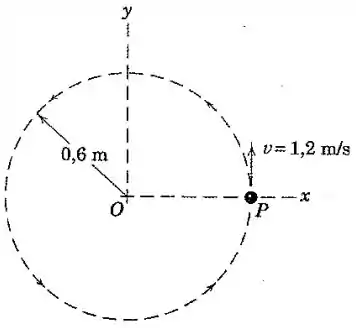
Uma partícula se desloca na trajetória circular mostrada. Desenhe o vetor aceleração e determine o seu módulo para os seguintes casos:
(a) a velocidade é e é constante,
(b) a velocidade é e está aumentando na taxa de cada segundo,
(c) a velocidade é e está diminuindo na taxa de cada segundo.
Em cada caso a partícula está na posição mostrada na figura.
Passo 1
(a) Galerinha, quando a velocidade é constante, não há aceleração tangencial. Isso significa que o vetor aceleração só terá a componente na direção normal, ou seja, ele estará apontado para o centro do círculo:
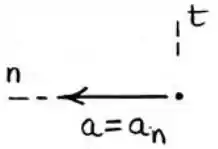
Então teremos:
Passo 2
(b) Agora a velocidade está aumentando a uma taxa constante. Isso significa que, além da componente normal, o vetor aceleração também terá a componente tangencial, apontando para o mesmo sentido da velocidade (para cima), pois a velocidade está aumentando:
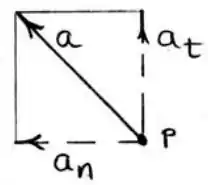
O enunciado desse item nos diz, em outras palavras, que a aceleração tangencial é:
E a aceleração normal será a mesma do item anterior, pois a velocidade e o raio são os mesmos:
Então o módulo será:
Passo 3
(c) Nesse caso aqui, a velocidade está diminuindo a uma taxa constante. Isso significa que, além da componente normal, o vetor aceleração também terá a componente tangencial, mas agora apontando para o sentido contrário da velocidade (para baixo), pois a velocidade está diminuindo:
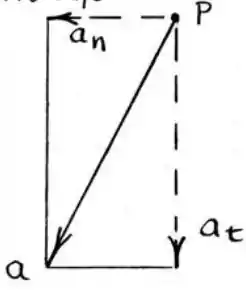
O enunciado desse item nos diz, em outras palavras, que a aceleração tangencial é:
E a aceleração normal será a mesma dos outros itens, pois a velocidade e o raio são os mesmos:
Então o módulo será:
Resposta
(a)
(b)
(c)