Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 14

Sabe-se que t = 2 s   e   t = 10 s a aceleração de uma partícula é inversamente proporcional ao cubo do tempo t . Quando t = 2 s ,   v = - 15 m / s e quando t = 10 s ,   v = 0,36 m / s . Sabendo que a partícula está duas vezes mais distante da origem quando t = 2 s do que quando t = 10 s , determine (a) a posição da partícula quando t = 2 s e quando t = 10 s , (b) a distância total percorrida pela partícula de t = 2 s   e   t = 10 s .

Passo 1

E ai gurizada tudo certinho? O enunciado pede que a gente determine a posição da partícula quando t = 2 s e quando t = 10 s , e a distância total percorrida pela partícula de t = 2 s   e   t = 10 s .

Temos: a = k t 3         k = c o n s t a n t e

Agora: d v d t = a = k t 3

Em: t = 2 s ,     v = - 15 m / s : ∫ - 15 v d v = ∫ 2 t k t 3 d t  

Ou v — 15 = k 2 2   x   1 t 2 - 1 2 2

Ou v = k 2   x   1 4 - 1 t 2 - 15 ( m / s )

Passo 2

Em: t = 10 s ,   v = 0,36   m / s : 0,36 = k 2   x   1 4 - 1 10 2 - 15

Ou k = 128   m ∙ s

E: v = 1 - 64 t 2 ( m / s )

Passo 3

  1. Temos: d x d t = v = 1 - 64 t 2

    2. Então: ∫ d x = ∫ 1 - 64 t 2 d t + C           C = c o n s t a n t e

    Ou x = t + 64 t + C m Agora: x 2 = 2 x 10 : 2 + 64 2 + C = 2   x   10 + 64 10 + C

    Ou C = 1,2   m e

    E: x = t + 64 t + 1,2 ( m )

    Em: t = 2 s : x 2 = 2 + 64 2 + 1,2

    t = 10 s : x 10 = 10 + 64 10 + 1,2

    Passo 3

    Galerinha existe uma segunda solução para o caso x 2 > 0 ,   x 10 < 0 . Para este caso,

    C = - 22   x 4 15 m .

    E: x 2 = 11   x 11 15 m ,       x 10 = - 5   x 13 15 m

    Passo 3

  2. Então: v = 0 1 - 64 t 2 = 0     o u     t = 8 s

Em: t = 8 s : x 8 = 8 + 64 8 + 1,2 = 17,2   m

Agora observe que: 2 s ≤ t < 8 s :     v < 0 8 s < t ≤ 10 s :     v > 0

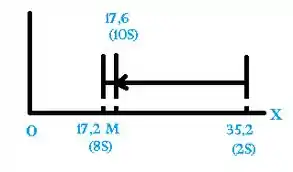
Então: x 8 - x 2 = 17,2 - 35,2 = 18 m x 10 - x 8 = 17,6 - 17,2 = 0,4 m

Distância total permitida = 18 + 0,4 m = 18,40 m

Importante dizer que a distância total percorrida é igual para ambos os casos.

Resposta

  1. x 2 = 35,2   m
  2. x 10 = 17,60   m

Distância total permitida = 18 + 0,4 m = 18,40 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento bidimensional de uma partícula e definido pelas relações r = 2b cos ω t e θ = ω t, onde b e ω são constantes. Determine (a) a velocidade e a aceleração da partícula em qualquer instante, (
A oscilação da haste OA em torno de O e definida pela relação θ = (2 / π ) (sen π t), onde θ e t são expressos em radianos e segundos, respectivamente. O cursor B desliza ao longo da haste de tal form
Para o estudo do desempenho de um carro de corrida posiciona-se uma câmera filmadora de alta velocidade no ponto A. A câmera e montada em um mecanismo que possibilita que ela grave o movimento do carr
Após a decolagem, um helicóptero sobe em linha reta em um ângulo constante de rampa β . Seu voo e rastreado por um radar localizado no ponto A. Determine a velocidade escalar do helicóptero em termos
O pino P está ligado a haste BC e desliza livremente ao longo da ranhura existente na haste AO. Determine a taxa de variação θ ˙ do ângulo θ , sabendo que BC se move com velocidade escalar constante v