Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 4
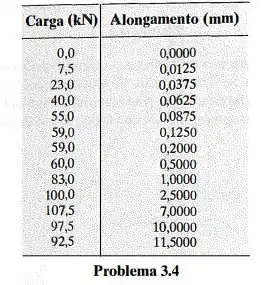
Um corpo de prova de aço com diâmetro original de e de comprimento de referência foi submetida a um ensaio de tração. Os dados resultantes são apresentados na tabela. Construa o gráfico do diagrama tensão-deformação e determine os valores aproximados do módulo de elasticidade, da tensão de escoamento, do limite de resistência e da tensão de ruptura. Use uma escala de e . Desenhe novamente a região elástica usando a mesma escala de tensão, mas use uma escala de deformação de .
Passo 1
Oláaaa, querido! O que ele quer aqui é que a gente faça o gráfico tensão – deformação com base nesses dados, de duas formas, usando duas escalas diferentes.
E depois a gente vai tirar alguns dados desses gráficos, que são: o módulo de elasticidade, a tensão de escoamento, o limite de resistência e a tensão de ruptura do material.
Vamos começar ajeitando nossos dados. Como a gente quer um gráfico tensão-deformação precisamos achar a tensão relativa a essas cargas. Para isso, devemos passar a carga dada na tabela para a tensão que ela gera utilizando a fórmula abaixo para todos os dados da tabela
Para acharmos , temos:
Onde
E também precisamos achar a deformação relativa a cada valor de alongamento que ele deu. Aí para acharmos a deformação , a gente aplica essa fórmula a todos os valores da segunda coluna:
Onde
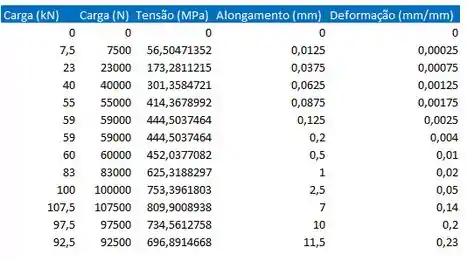
Nossos dados ficam assim:
Passo 2
Agora é esboçar o diagrama tensão-deformação, que é uma função . Fica assim
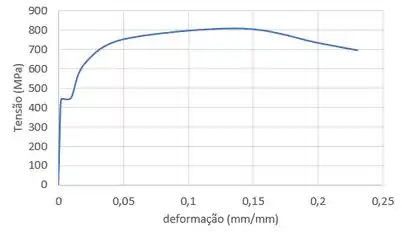
Aqui a gente usou o espaçamento de que ele pediu na deformação. O que ele quer dizer com é que se você for desenhar o gráfico a mão, você vai colocar o espaçamento de na folha como sendo de .
O mesmo vale para . Não significa que você vai marcar os valores no seu gráfico de em , mas que uma variação de tem na sua folha. A gente não vai fazer isso aqui porque fazemos o gráfico no computador, tá?
Mas percebe que ali no começo do gráfico que os dados estão bem encolhidos, né? Por isso que ele pediu para fazer essa parte do começo, onde nós estamos no regime elástico e nosso gráfico é uma reta, com uma escala diferente. Fica assim:
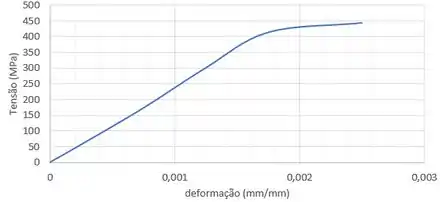
Percebe que fizemos até um pouco além do regime elástico porque passamos um pouco da parte em que ele é reto. E se for fazer esse a mão, agora o intervalo de equivale a na sua folha, tá?
Passo 3
Vamos tirar as informações desse gráfico agora.
Ele quer a tensão de escoamento. Essa é a tensão limite para a primeira reta do nosso gráfico. Ou seja, é o valor de onde o gráfico deixa de ser reto pela primeira vez.
Vemos no gráfico que a gente fez que essa tensão vale aproximadamente:
Ele quer o módulo de elasticidade do nosso material também.
Para calcularmos o módulo de elasticidade, podemos usar os valores de e de qualquer ponto do diagrama que siga a Lei de Hooke, ou seja, de um ponto que esteja na reta inicial do segundo gráfico que a gente fez.
Vamos usar o ponto onde porque ele pertence também a reta. Nele vemos que pelo gráfico:
Aí é substituir esses pontos na lei de na Lei de Hooke
Passo 4
Ele quer também o limite de resistência e a tensão de ruptura.
A tensão de ruptura é a última tensão que aparece no gráfico completo, na maior deformação. Pelo nosso gráfico que mostra todos os pontos, temos que
E o limite de resistência é a tensão máxima que suporta. Vemos que pelo gráfico completo, a tensão máxima está em torno de:
Obs: Devido a forma de desenhar o gráfico e até na forma de se extrair os dados do gráfico, podem haver diferenças entre os valores que a gente achou, que você pode achar sozinho e os do gabrito.
Mas como estamos falando de gráficos e temos essas incertezas, valores próximos a esses e próximos ao que o gabarito diz são consideráveis. Então estamos certinhos, tá?