Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 1
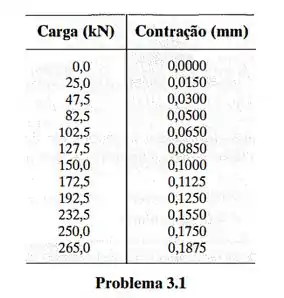
Um cilindro de concreto com de diâmetro e de comprimento de referência é testado sob compressão. Os resultados do ensaio são apresentados na tabela como carga em relação à contração. Desenhe o diagrama tensão-deformação usando escalas de e . Use o diagrama para determinar o módulo de elasticidade aproximado.
Passo 1
O exercício quer que a gente determine o módulo de elasticidade desse material.
Então, devemos desenhar o Diagrama Tensão-Deformação do material. Para isso, devemos passar a carga dada na tabela para a tensão utilizando a fórmula abaixo para todos os dados da tabela
Passo 2
Para acharmos , temos:
Passo 3
E para acharmos a deformação :
Onde:
- é a deformação
- é a variação do comprimento
- o comprimento inicial
Para uma carga de por exemplo vamos ter uma contração de 0,05 mm, ou seja, .
Assim podemos calcular a deformação:
Mas isso não é o bastante porque queremos fazer um gráfico com a tensão e não a carga. Logo a tensão é:
E assim por diante, para todos os pontos.
Passo 4
Agora é só esboçar o diagrama tensão-deformação, que nada mais é do que uma função . Fica assim
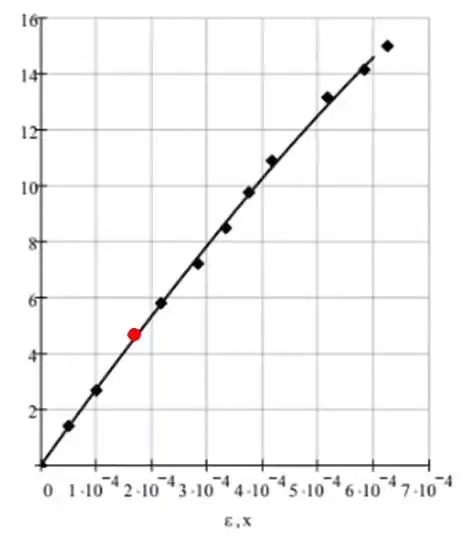
O ponto dado como exemplo no passo anterior está marcado em vermelho.
Passo 5
Para calcularmos o módulo de elasticidade, podemos usar os valores de e de qualquer ponto do diagrama que siga a Lei de Hooke (ou seja, enquanto o gráfico é uma reta).
Substituindo na Lei de Hooke
Utilizando o ponto onde e