Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 42
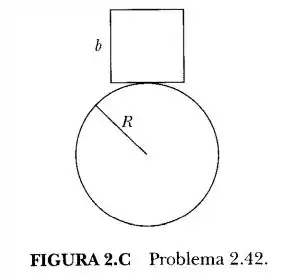
Um cubo sólido de densidade uniforme e lados com dimensão b se encontra em equilíbrio na parte superior de um cilindro de raio R (Figura 2.C). Os planos dos quatro lados do cubo são paralelos ao eixo do cilindro. O contato entre o cubo e o cilindro é perfeitamente áspero. Sob quais condições o equilíbrio é estável ou não estável?
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de mecânica Newtoniana.
Diagramando a situação problema:
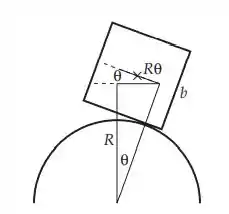
A partir da figura temos:
E a energia potencial é dada por:
Daí, teremos que:
Passo 2
O ponto de equilíbrio (onde dEpot/dθ = 0) que desejamos observar é claramente θ = 0. Nesse ponto, temos d2Epot/dθ2 = mg(R – b/2), que é estável para R > b/2 e instável para R b/2 e instável para R ≤ b/2.
Resposta
Ver passo a passo.