Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas de Revisão - Ex. 193

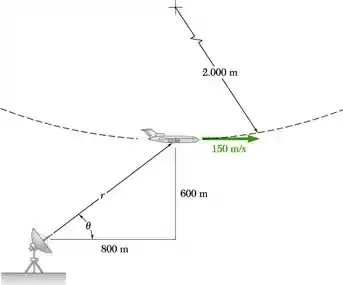
Na parte baixa do loop em um plano vertical, um aeroplano tem velocidade de 150 m/s e está acelerando a uma taxa de 25 m/s2. O raio de curvatura do loop é 2.000 m. O aeroplano está sendo controlado pelo radar em O. Qual é o valor registrado de r ˙ , r ¨ , θ ˙ e θ ¨ para esse instante?

Passo 1

O exercício pede que a gente encontre valor registrado de r ˙ , r ¨ , θ ˙ e θ ¨ para esse instante

Geometria. As coordenadas polares são

v = 800 2 + 600 2 = 1000   m             θ = tan - 1 600 800 = 36.87 °

Análise de velocidade.

v = 150   m/s   →

v r = 150 cos ⁡ θ = 120   m/s

v θ = - 150 sin ⁡ θ = - 90   m/s

v r = r ˙

v θ = r θ ˙             θ ˙ = v θ r = - 90 1000

Passo 2

Análise de aceleração.

a t = 25   m/ s 2

a n = v 2 ρ = 150 2 2000 = 11.25   m/ s 2

a = 25   m/ s 2 → + 11.25   m/ s 2 ↑   = 27.41   m/ s 2     24.23 °

β = 24.23 °

θ - β = 12.64 °

Passo 3

a r = a cos ⁡ θ - β = 27.41 cos ⁡ 12.64 ° = 26.74   m/ s 2

a θ = - a sin ⁡ θ - β = - 27.41 sin ⁡ 12.64 ° = - 6.00   m/ s 2

a r = r ¨ - r θ ˙ 2             r ¨ = a r + r θ ˙ 2

r ¨ = 26.74 + 1000 0.0900 2

a θ = r θ ¨ + 2 r ˙ θ ˙

θ ¨ = a θ r - 2 r ˙ θ ˙ r = - 6.00 1000 - 2 120 - 0.0900 1000

Resposta

r ˙ = 120   m/s

θ ˙ = - 0.0900   rad/s

r ¨ = 34.8   m/ s 2

θ ¨ = - 0.0156   rad/ s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um menino lança uma bola para cima com uma velocidade v 0 = 12m / s . O vento transmite uma aceleração horizontal de 0,4m / s 2 para a esquerda. Em que ângulo θ a bola deve ser atirada para que esta r
O jogador de basquete gosta de arremessar seu lance livre em um ângulo θ = 50 ° com a horizontal como mostrado. Que velocidade inicial v 0 fará com que a bola passe através do centro do aro?
A velocidade de disparo de um fuzil de longo alcance em A é u = 400m / s . Determine os dois ângulos de elevação θ , que permitirão ao projétil acertar a montanha no alvo B .
Um projétil é lançado a partir do ponto A com uma velocidade inicial v 0 = 30m / s . Determine o valor mínimo do ângulo de lançamento α com o qual o projétil cairá no ponto B .
Uma equipe de estudantes de engenharia está projetando uma catapulta para lançar uma pequena bola em A de modo que esta caia na caixa. Sabendo que o vetor velocidade inicial faz um ângulo de 30 ° com