Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 1.Problemas - Ex. 7
Considere um cubo unitário com um vértice na origem e três lados adjacentes colocados ao longo dos três eixos de um sistema de coordenadas retangulares. Encontre os vetores que descrevem as diagonais do cubo. Qual é o ângulo entre qualquer par diagonais?
Passo 1
Oi galera !!, vamos responder mais uma questão do nosso livro de Dinâmica clássica de partículas e sistemas.
Para essa questão vamos primeiro desenhar nosso cubo. Para isso, vamos propor nosso eixo de origem e como também as dimensões do cubo.
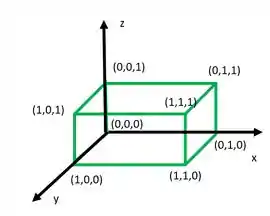
Vamos, agora para o próximo passo e encontrar os valores das diagonais do cubo.
Passo 2
Galera, lembrando um pouco de álgebra, podemos encontrar a diagonal do cubo.
E no total, serão 4 diagonais para serem descobertas.
é o ponto de origem até o ponto
é ponto até o ponto
é o ponto até o ponto
é o ponto até o ponto
Passo 3
Estamos quase lá, vamos encontrar o modulo desse vetores
=
Assim, usando a relação entre os vetores podemos encontrar o ângulo para qualquer umas das diagonais,
= cos
= 70.5°
Passo 4
Como comentado anteriormente, podemos realizar uma extrapolação para as próximas diagonais,
= == = =
Resposta
Assim, encontramos que para um cubo, o ângulo será igual a,
=70.5°
Espero que ajudem nos estudos, até próxima