Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 35
Efetue os cálculos numéricos do Exemplo 2.7 para os valores fornecidos na Figura 2.8. Elabore os gráficos das Figuras 2.8 e 2.9. Não duplique a solução no Apêndice H: Elabore a sua própria solução.
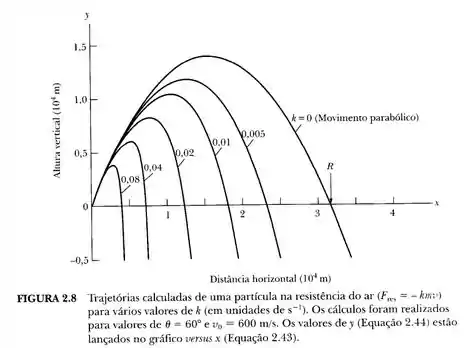
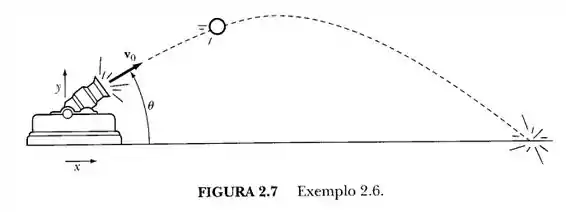
Exemplo 2.7: A seguir, adicionamos o efeito da resistência ao movimento do projétil no exemplo anterior. Calcule a redução no alcance sob a premissa de que a força provocada pela resistência do ar é diretamente proporcional à velocidade do projétil.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de mecânica Newtoniana.
Para responder ao questionamento do enunciado, temos as condições iniciais:
As equações de movimento são:
Que possuem soluções:
Passo 2
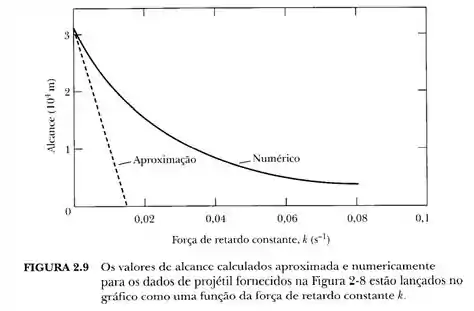
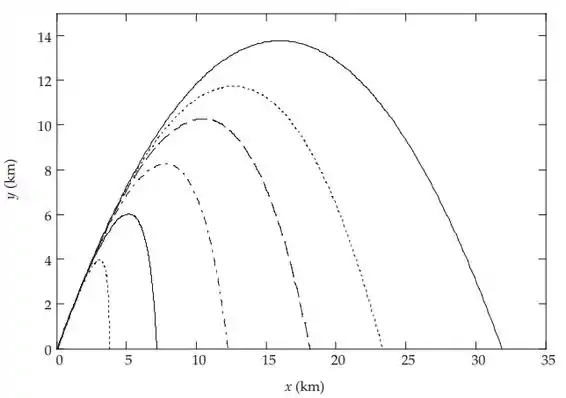
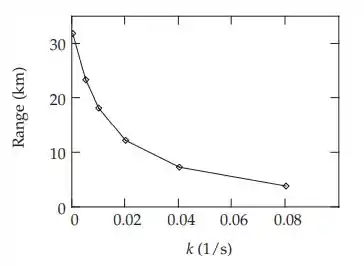
Somos solicitados a resolver as Equações (I) e (II), para os valores k = 0, k = 0,005, k = 0,01, k = 0,02, k = 0,04 e k = 0,08 (todos em s-1), com velocidade inicial v0 = 600 m/s e ângulo de elevação θ = 60°. A primeira figura é produzida pela solução numérica das equações diferenciais e concorda muito com a Figura 2-8. A Figura 2-9 pode ser reproduzida mais de perto encontrando o intervalo para nossos valores de k e plotando-os vs k. Uma curva suave poderia ser desenhada, ou mais intervalos poderiam ser calculados com mais valores de k para preencher o gráfico, mas escolhemos aqui apenas conectar os pontos com linhas retas.
Resposta
Ver passo a passo.